
【题目】如图,在平面直角坐标系中,![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() 在
在![]() 轴的负半轴上,顶点
轴的负半轴上,顶点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() ,线段
,线段![]() 的垂直平分线分别交
的垂直平分线分别交![]() 于点
于点![]() .
.
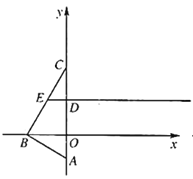
(1)点![]() 的坐标;
的坐标;
(2)点![]() 为线段
为线段![]() 的延长线上的一点,连接
的延长线上的一点,连接![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,点![]() 为线段
为线段![]() 的延长线上一点,连接
的延长线上一点,连接![]() ,若
,若![]() ,求
,求![]() 的度数.
的度数.
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=5 cm,BC=7 cm,点P从点A开始沿AB边向点B以1 cm/s的速度移动,同时点Q从点B开始沿BC向点C以2cm/s的速度移动.当一个点到达终点时另一点也随之停止运动,运动时间为x秒(x>0).
(1)求几秒后,PQ的长度等于5 cm.
(2)运动过程中,△PQB的面积能否等于8 cm2?并说明理由.
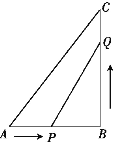
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将线段 AB 先向右平移 5 个单位,再将所得线段绕原点按顺时针方向旋转 90°,得到线段 AB ,则点 B 的对应点 B′的坐标是( )
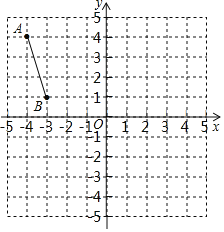
A.(-4 , 1)B.( -1, 2)C.(4 ,- 1)D.(1 ,- 2)
查看答案和解析>>
科目:初中数学 来源: 题型:
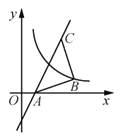
【题目】如图,过点C(3,4)的直线![]() 交
交![]() 轴于点A,∠ABC=90°,AB=CB,曲线
轴于点A,∠ABC=90°,AB=CB,曲线![]() 过点B,将点A沿
过点B,将点A沿![]() 轴正方向平移
轴正方向平移![]() 个单位长度恰好落在该曲线上,则
个单位长度恰好落在该曲线上,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂生产A,B两种产品,其单价随市场变化而做相应调整,营销人员根据前三次单价变化的情况,绘制了如下统计表及不完整的折线图: A,B产品单价变化统计表
第一次 | 第二次 | 第三次 | |
A产品单价 (元/件) | 6 | 5.2 | 6.5 |
B产品单价 (元/件) | 3.5 | 4 | 3 |

并求得了A产品三次单价的平均数和方差:![]() ;
;![]()
(1)补全图中B产品单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %;
(2)求B产品三次单价的方差,并比较哪种产品的单价波动小;
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0)使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
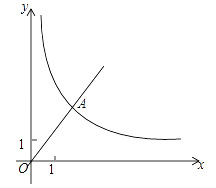
【题目】已知:如图,在平面直角坐标系中,正比例函数y=![]() 的图象经过A,点A的纵坐标为4,反比例函数y=
的图象经过A,点A的纵坐标为4,反比例函数y=![]() 的图象也经过点A,在第一象限内的点B在这个反比例函数图象上,过点B做BC∥x轴,交y轴于点C,且AC=AB,求:
的图象也经过点A,在第一象限内的点B在这个反比例函数图象上,过点B做BC∥x轴,交y轴于点C,且AC=AB,求:
(1)这个反比例函数的解析式;
(2)ΔABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,M、N分别在AD、BC上,且AM=CN,连接MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为( )
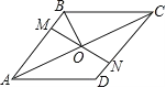
A.28°B.56°C.62°D.72°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,

(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,横、纵坐标都为整数的点称为整点.已知一组正方形的四个顶点恰好落在两坐标轴上,请你观察每个正方形四条边上的整点的个数的变化规律.回答下列问题:
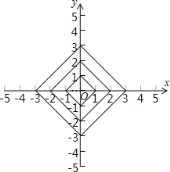
(1)经过x轴上点(5,0)的正方形的四条边上的整点个数是________;
(2)经过x轴上点(n,0)(n为正整数)的正方形的四条边上的整点个数为_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com