
����Ŀ��ij������A��B���ֲ�Ʒ���䵥�����г��仯������Ӧ������Ӫ����Ա����ǰ���ε��۱仯�����������������ͳ�Ʊ���������������ͼ�� A��B��Ʒ���۱仯ͳ�Ʊ�
��һ�� | �ڶ��� | ������ | |
A��Ʒ���� (Ԫ/��) | 6 | 5.2 | 6.5 |
B��Ʒ���� (Ԫ/��) | 3.5 | 4 | 3 |

�������A��Ʒ���ε��۵�ƽ�����ͷ��![]() ��
��![]()
(1)��ȫͼ��B��Ʒ���۱仯������ͼ��B��Ʒ�����εĵ��۱���һ�εĵ��۽����� %��
(2)��B��Ʒ���ε��۵ķ�����Ƚ����ֲ�Ʒ�ĵ��۲���С��
(3)�ó��������Ĵε��ۣ�A��Ʒ�ĵ�����Ϊ6.5Ԫ/����B��Ʒ�ĵ��۱�3Ԫ/���ϵ�m%(m>0)ʹ��A��Ʒ���Ĵε��۵���λ����B��Ʒ�Ĵε�����λ����2����1����m��ֵ��
���𰸡���1������ͼ��������![]() ����2��
����2��![]() ��B��Ʒ�ĵ��۲���С����3��
��B��Ʒ�ĵ��۲���С����3��![]()
��������
��1��������Ŀ�ṩ���ݲ�������ͳ��ͼ�ͼ��㽵�۰ٷֱȼ��ɣ�
��2���ֱ����ƽ����������ɣ�
��3������ȷ�����Ĵε��۵���λ����Ȼ��ȷ�����Ĵε��۵ķ�Χ�����ݡ�A��Ʒ���Ĵε��۵���λ����B��Ʒ�Ĵε�����λ����2����1����ʽ��m����.
��1����ȫ�������ͼ����ͼ2��ʾ��
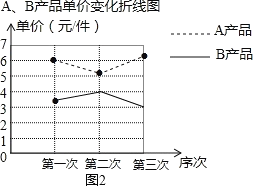
B��Ʒ�����εĵ��۱���һ�εĵ��۽����ˣ�![]()
���![]() ��
��
��2��![]()
![]()
��B��Ʒ�ķ���С��
��B��Ʒ�ĵ��۲���С��
��3�����Ĵε��ۺ���A��Ʒ�����Ĵε��۵���λ��Ϊ��![]()
���Ĵε��ۺ�B��Ʒ�ĵ���Ϊ��![]()
�ٵ�![]() ʱ������ɵã�
ʱ������ɵã�![]()
��ã�![]()
�ڵ�![]() ʱ��B��Ʒ�Ĵε�����λ����2����1Ϊ��
ʱ��B��Ʒ�Ĵε�����λ����2����1Ϊ��![]()
��![]()
��![]() ��
��
��![]() ��ֵ��
��ֵ��![]() .
.


 ����������ϵ�д�
����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ͬѧ����ѧϰԲ�Ļ�������ʱ������һ�����ۣ���ͼ1��Բ![]() ��
��![]() ��
��![]() ��Բ�е������ң�
��Բ�е������ң�![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ����
����![]() .
.
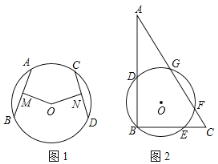
��1�����С��֤��������ۣ�
��2����ο�С��˼������ķ���������⣬��ͼ2����![]() �У�
��![]() ��
��![]() Ϊ
Ϊ![]() �����ģ���
�����ģ���![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ��
Ϊ�뾶��Բ��![]() ���߷ֱ��ཻ�ڵ�
���߷ֱ��ཻ�ڵ�![]() ��
��![]() ��
��![]() ��
��![]() . ��
. ��![]() ��
��![]() ����
����![]() ���ܳ�.
���ܳ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ�������⣮
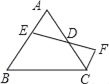
С����̽����������λ�����ʶ���֤���Ĺ����У��õ���������ʾ��һ���߶ξ�����һ�߶ε��е㣬���ӳ�ǰ�ߣ����ҳ�����ȣ����ܹ���ȫ�������Σ���ͼ��D����ABC��AC�ߵ��е㣬EΪAB����һ�㣬�ӳ�ED��F��ʹDF��DE������CF����ɵ���CFD�ա�AED���Ӷ�����ABC��ƴ�������ȵ��ı���BCFE�����ܴ�С�ϵķ�˼�еõ���ʾ��
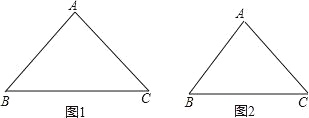
��1����ͼ1����֪��ABC�����ż�һ����ʹ�õ�������ͼ����ƴ��ƽ���ı��Σ�
�ٰѼ����ߺ�ƴ�ɵ�ƽ���ı��λ���ͼ1�ϣ���ָ��������Ӧ���ϵ�������
��˼�����ش�Ҫʹ������ƴ�õ���ƽ���ı��γ�Ϊ���Σ���ABC�ı��Ӧ����ʲô�����������أ��������أ���ֱ��д���÷��ű�ʾ��������
��2����ͼ2����֪�����ABC�����ż�������ʹ�õ�������ͼ����ƴ�ɾ��Σ��Ѽ����ߺ�ƴ�ɵľ��λ���ͼ2�ϣ���ָ��������Ӧ���ϵ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ���C������Ϊ��4����1����
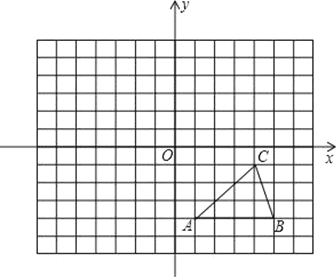
��1������ABC����ƽ��5����λ��õ���Ӧ����A1B1C1��������A1B1C1����д��A1�����ꣻ
��2����ԭ��OΪ�Գ����ģ��ٻ�������A1B1C1����ԭ��O�ԳƵ���A2B2C2����д����A2������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ƽ��ͼ��S����P��Q��S���������㣬���ǰ��߶�PQ�ij��ȵ����ֵ��Ϊƽ��ͼ��S���������������磬�����εĿ���������ĶԽ��ߵij��ȣ�
��1��д������ͼ�εĿ��ࣺ
�ٰ뾶Ϊ1��Բ���� ����
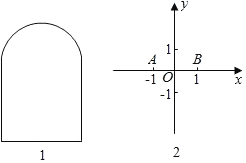
����ͼ1���Ϸ��ǰ뾶Ϊ1�İ�Բ���·��������ε������ߵ��������������� ����
��2����ͼ2����ƽ��ֱ������ϵ�У���֪��A����1��0����B��1��0����C������ƽ���ڵĵ㣬����AB��BC��CA���γɵ�ͼ��ΪS����S�Ŀ���Ϊd��
����d��2�����C���ڵ�����������
������C�ڡ�M���˶�����M�İ뾶Ϊ1��Բ��M�ڹ��㣨0��2������y�ᴹֱ��ֱ���ϣ����ڡ�M�������C������5��d��8��ֱ��д��Բ��M�ĺ�����x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
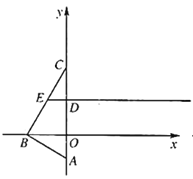
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() �Ķ���
�Ķ���![]() ������Ϊ
������Ϊ![]() ������
������![]() ��
��![]() ��ĸ������ϣ�����
��ĸ������ϣ�����![]() ��
��![]() ����������ϣ���
����������ϣ���![]() ���߶�
���߶�![]() �Ĵ�ֱƽ���߷ֱ�
�Ĵ�ֱƽ���߷ֱ�![]() �ڵ�
�ڵ�![]() .
.
��1����![]() �����ꣻ
�����ꣻ
��2����![]() Ϊ�߶�
Ϊ�߶�![]() ���ӳ����ϵ�һ�㣬����
���ӳ����ϵ�һ�㣬����![]() �����
�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3���ڣ�2���������£���![]() Ϊ�߶�
Ϊ�߶�![]() ���ӳ�����һ�㣬����
���ӳ�����һ�㣬����![]() ����
����![]() ����
����![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������ĺ����װ���ĸ��ֱ��������![]() ��
��![]() ��
��![]() ��
��![]() ��С�����ǵ���״����С���ʵص���ȫ��ͬ.Сǿ�ȴӺ��������ȡ��һ��С��������Ϊx���Żغ���ҡ�Ⱥ�����С�����ȡ��һ��С��������Ϊy.
��С�����ǵ���״����С���ʵص���ȫ��ͬ.Сǿ�ȴӺ��������ȡ��һ��С��������Ϊx���Żغ���ҡ�Ⱥ�����С�����ȡ��һ��С��������Ϊy.
��1�����б�������״ͼ��ʾ����x��y�������п��ܳ��ֵĽ����
��2����Сǿ��С����ȡһ��С����ȷ���ĵ㣨x��y������һ�κ���![]() ��ͼ���ϵĸ��ʣ�
��ͼ���ϵĸ��ʣ�
��3����Сǿ��С����ȡһ��С����ȷ������x��y����![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η���x2+��2m+1��x+m2��1=0����������ȵ�ʵ������
��1����m��ȡֵ��Χ��
��2��д��һ������������m��ֵ�������ʱ���̵ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
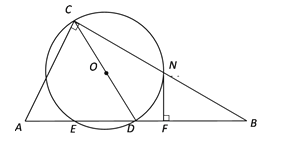
����Ŀ����ͼ����Rt��ABC�У���ACB��90������б��AB�ϵ�����CDΪֱ������O����AC��BC�ֱ��ڵ�M��N����AB����һ������ΪE������N��NF��AB������ΪF��
��1����֤��NF�ǡ�O�����ߣ�
��2����NF��2��DF��1������ED�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com