
����Ŀ����һ�������ĺ����װ���ĸ��ֱ��������![]() ��
��![]() ��
��![]() ��
��![]() ��С�����ǵ���״����С���ʵص���ȫ��ͬ.Сǿ�ȴӺ��������ȡ��һ��С��������Ϊx���Żغ���ҡ�Ⱥ�����С�����ȡ��һ��С��������Ϊy.
��С�����ǵ���״����С���ʵص���ȫ��ͬ.Сǿ�ȴӺ��������ȡ��һ��С��������Ϊx���Żغ���ҡ�Ⱥ�����С�����ȡ��һ��С��������Ϊy.
��1�����б�������״ͼ��ʾ����x��y�������п��ܳ��ֵĽ����
��2����Сǿ��С����ȡһ��С����ȷ���ĵ㣨x��y������һ�κ���![]() ��ͼ���ϵĸ��ʣ�
��ͼ���ϵĸ��ʣ�
��3����Сǿ��С����ȡһ��С����ȷ������x��y����![]() �ĸ���.
�ĸ���.
���𰸡���1�������������
��2��P��������һ�κ�����ͼ���ϣ�=![]() ��
��
��3��P��![]() ��=
��=![]() ��
��
��������
��1���б��ó����еȿ��ܵ���������ɣ�
��2���ҳ���ȷ���ĵ㣨x��y������һ�κ���y=x��1��ͼ���ϵ�������������������ĸ��ʣ�
��3���ҳ���ȷ������x��y����y=x��1��������������������ĸ��ʣ�
��1���б����£�
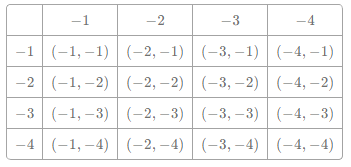
��2�����еȿ��ܵ������16�֣�������ȷ���ĵ㣨x��y������һ�κ���y=x��1�������3�֣��ֱ�Ϊ����1����2��������2����3��������3����4������P��������һ�κ�����ͼ���ϣ�=![]() ��
��
��3����Сǿ��С����ȡһ��С����ȷ������x��y����y>x1���У�(1,1),(2,1),(2,2),(3,1),(3,2),(3,3),(4,1),(4,2),(4,3),(4,4)��
��Сǿ��С����ȡһ��С����ȷ������x��y����y>x1�ĸ���Ϊ��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
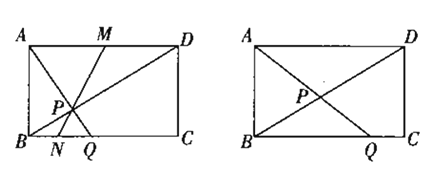
����Ŀ����ͼ������ABCD�У�AB=a,AD=b,��P�ǶԽ���BD�ϵ�һ�����㣨��P����B��D�غϣ�������AP���ӳ�������BC�ڵ�Q��
��1����AP��BDʱ������ABQ��������ú�a��b�Ĵ���ʽ��ʾ��.
��2������MΪAD�ߵ��е㣬����MP��BC�ڵ�N��֤������NҲΪ�߶�BQ���е�.
��3����ͼ����![]() Ϊ��ֵʱ����ADP����BPQ�����֮����С.
Ϊ��ֵʱ����ADP����BPQ�����֮����С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��a��0�Գ���Ϊֱ��x��1����x���һ����������Ϊ����1��0�����䲿��ͼ����ͼ��ʾ�����н��ۣ���abc��0����4ac��b2���۷���ax2+bx+c��0����������x1����1��x2��3����3a+c��0���ݵ�y��0ʱ��x��ȡֵ��Χ�ǩ�1��x��3�����н�����ȷ�ĸ����ǣ�������
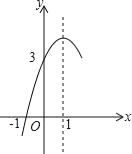
A. 1��B. 2��C. 3D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������A��B���ֲ�Ʒ���䵥�����г��仯������Ӧ������Ӫ����Ա����ǰ���ε��۱仯�����������������ͳ�Ʊ���������������ͼ�� A��B��Ʒ���۱仯ͳ�Ʊ�
��һ�� | �ڶ��� | ������ | |
A��Ʒ���� (Ԫ/��) | 6 | 5.2 | 6.5 |
B��Ʒ���� (Ԫ/��) | 3.5 | 4 | 3 |

�������A��Ʒ���ε��۵�ƽ�����ͷ��![]() ��
��![]()
(1)��ȫͼ��B��Ʒ���۱仯������ͼ��B��Ʒ�����εĵ��۱���һ�εĵ��۽����� %��
(2)��B��Ʒ���ε��۵ķ�����Ƚ����ֲ�Ʒ�ĵ��۲���С��
(3)�ó��������Ĵε��ۣ�A��Ʒ�ĵ�����Ϊ6.5Ԫ/����B��Ʒ�ĵ��۱�3Ԫ/���ϵ�m%(m>0)ʹ��A��Ʒ���Ĵε��۵���λ����B��Ʒ�Ĵε�����λ����2����1����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�BC�Ĵ�ֱƽ����EF����ABC��ƽ����BD��E�������BAC=60�㣬��ACE=24�㣬��ô��BCE�Ĵ�С�ǣ�������

A. 24�� B. 30�� C. 32�� D. 36��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�M��N�ֱ���AD��BC�ϣ���AM=CN������MN��AC���ڵ�O������BO������DAC=28�������OBC�Ķ���Ϊ( )
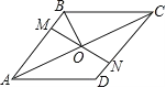
A.28��B.56��C.62��D.72��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ͬһƽ���ڣ�������ȫ�ȵĵ���ֱ��������ABC��AFG�ڷ���һ��AΪ�������㣬��BAC=��AGF=90����AB=4.����ABC�̶���������AFG�Ƶ�A��ת��AF��AG���BC�Ľ���ֱ�ΪD��E(��D�����B�غϣ���E�����C�غ�).
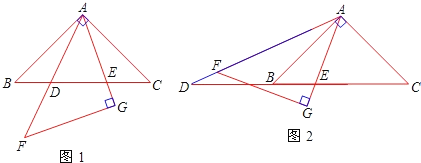
(1)��֤����ABE����DCA��
(2)��BE��CD=k��kΪ����������k��ֵ��
(3)����ת�����У�����AFG��ת����ͼ2��λ��ʱ��AG��BC���ڵ�E��AF���ӳ�����CB���ӳ��߽��ڵ�D����ô��2����k��ֵ�Ƿ����˱仯?Ϊʲô?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ȫ��ͼ1������ʹ��ˮ���������ֵĽ�������仯���仯��ij��������Ȫ��״�������ߣ������ˮ��Ϊԭ�㣬��ˮ���밶��18m�����ֱ仯ʱ�������ߵĶ�����ֱ��y=kx�ϱ䶯���Ӷ�����һ�鲻ͬ�������ߣ�ͼ2�������������ߵ�ͳһ��ʽΪy=ax2+bx��
��1������֪k=1���������������ˮ�����߶ȴ�3m�����ʱa��b��ֵ��
��2����k=1�������ˮǡ�ôﵽ���ߣ����ʱ�����������ˮ�����߶��Ƕ����ף�
��3����k=3��a=��![]() ���������������ˮ���ܷ�ﵽ���ߣ�
���������������ˮ���ܷ�ﵽ���ߣ�
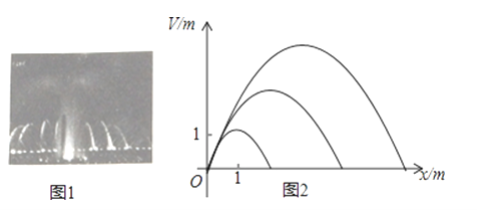
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C��D��Բ�ϣ�![]() ������C��CE��AD��AD���ӳ����ڵ�E��
������C��CE��AD��AD���ӳ����ڵ�E��
��1����֤��CE�ǡ�O�����ߣ�
��2����֪BC��3��AC��4����CE�ij���
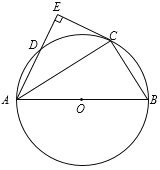
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com