
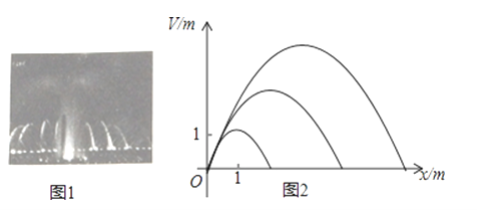
【题目】音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a、b的值;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若k=3,a=﹣![]() ,则喷出的抛物线水线能否达到岸边?
,则喷出的抛物线水线能否达到岸边?
【答案】(1)a、b的值分别是![]() ,2;(2)喷出的抛物线水线最大高度是9米;(3)喷出的抛物线水线能达到岸边.
,2;(2)喷出的抛物线水线最大高度是9米;(3)喷出的抛物线水线能达到岸边.
【解析】
(1)根据抛物线的顶点在直线y=kx上,抛物线为y=ax2+bx,k=1,且喷出的抛物线水线最大高度达3m,可以求得a,b的值;
(2)根据k=1,喷出的水恰好达到岸边,抛物线的顶点在直线y=kx上,可以求得抛物线的对称轴x的值,从而可以得到此时喷出的抛物线水线最大高度;
(3)根据k=3,a=-![]() ,抛物线的顶点在直线y=kx上,抛物线为y=ax2+bx,可以求得b的值,然后令y=0代入抛物线的解析式,求得x的值,然后与18作比较即可解答本题.
,抛物线的顶点在直线y=kx上,抛物线为y=ax2+bx,可以求得b的值,然后令y=0代入抛物线的解析式,求得x的值,然后与18作比较即可解答本题.
(1)∵y=ax2+bx的顶点为(﹣![]() ),抛物线的顶点在直线y=kx上,k=1,抛物线水线最大高度达3m,
),抛物线的顶点在直线y=kx上,k=1,抛物线水线最大高度达3m,
∴![]() ,
,![]() ,
,
解得,a=![]() ,b=2,
,b=2,
即k=1,且喷出的抛物线水线最大高度达3m,此时a、b的值分别是![]() ,2;
,2;
(2)∵k=1,喷出的水恰好达到岸边,出水口离岸边18m,抛物线的顶点在直线y=kx上,
∴此时抛物线的对称轴为x=9,y=x=9,
即此时喷出的抛物线水线最大高度是9米;
(3)∵y=ax2+bx的顶点为(﹣![]() )在直线y=3x上,a=﹣
)在直线y=3x上,a=﹣![]() ,
,
∴![]() ,
,
解得,b=6,
∴抛物线y=![]() ,
,
当y=0时,0=![]() ,
,
解得,x1=21,x2=0,
∵21>18,
∴若k=3,a=﹣![]() ,则喷出的抛物线水线能达到岸边,
,则喷出的抛物线水线能达到岸边,
即若k=3,a=﹣![]() ,喷出的抛物线水线能达到岸边.
,喷出的抛物线水线能达到岸边.


科目:初中数学 来源: 题型:
【题目】阅读材料,解决问题.
小聪在探索三角形中位线性质定理证明的过程中,得到了如下启示:一条线段经过另一线段的中点,则延长前者,并且长度相等,就能构造全等三角形.如图,D是△ABC的AC边的中点,E为AB上任一点,延长ED至F,使DF=DE,连接CF,则可得△CFD≌△AED,从而把△ABC剪拼成面积相等的四边形BCFE.你能从小聪的反思中得到启示吗?
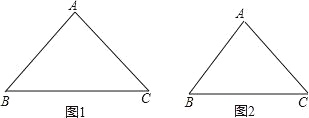
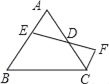
(1)如图1,已知△ABC,试着剪一刀,使得到的两块图形能拼成平行四边形.
①把剪切线和拼成的平行四边形画在图1上,并指出剪切线应符合的条件.
②思考并回答:要使上述剪拼得到的平行四边形成为矩形,△ABC的边或角应符合什么条件?菱形呢?正方形呢?(直接写出用符号表示的条件)
(2)如图2,已知锐角△ABC,试着剪两刀,使得到的三块图形能拼成矩形,把剪切线和拼成的矩形画在图2上,并指出剪切线应符合的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() 的小球,它们的形状、大小、质地等完全相同.小强先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
的小球,它们的形状、大小、质地等完全相同.小强先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(x,y)落在一次函数![]() 的图象上的概率;
的图象上的概率;
(3)求小强、小华各取一次小球所确定的数x、y满足![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
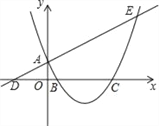
【题目】如图,已知直线y=![]() x+1与y轴交于点A,与x轴交于点D,抛物线y=
x+1与y轴交于点A,与x轴交于点D,抛物线y= ![]() x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标__________.
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
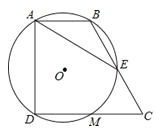
【题目】如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:
①DM=CM;②弧AB=弧EM;③⊙O的直径为2;④AE=AD.
其中正确的结论有______(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
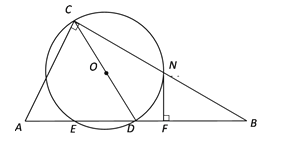
【题目】如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作⊙O,与AC、BC分别交于点M、N,与AB的另一个交点为E.过点N作NF⊥AB,垂足为F.
(1)求证:NF是⊙O的切线;
(2)若NF=2,DF=1,求弦ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c与x轴交于点A(﹣2,0)
(1)填空:c= ;(用含b的式子表示)
(2)b<4.
①求证:抛物线与x轴有两个交点;
②设抛物线与x轴的另一个交点为B,当线段AB上恰有5个整点(横坐标、纵坐标都是整数的点),求b的取值范围;
(3)平移抛物线,使其顶点P落在直线y=3x﹣2上,设抛物线与直线的另一个交点为Q,C在该直线下方的抛物线上,求△CPQ面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com