
【题目】如图,已知直线y=![]() x+1与y轴交于点A,与x轴交于点D,抛物线y=
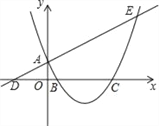
x+1与y轴交于点A,与x轴交于点D,抛物线y= ![]() x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标__________.
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标__________.
【答案】![]()
【解析】分析:易得点A(0,1),那么把A,B坐标代入y=![]() x2+bx+c即可求得函数解析式,然后求出对称轴,找到C关于对称轴的对称点B,连接AB交对称轴的一点就是M.应让过AB的直线解析式和对称轴的解析式联立即可求得点M坐标.
x2+bx+c即可求得函数解析式,然后求出对称轴,找到C关于对称轴的对称点B,连接AB交对称轴的一点就是M.应让过AB的直线解析式和对称轴的解析式联立即可求得点M坐标.
详解: (1)将A(0,1)、B(1,0)坐标代入y=![]() x2+bx+c,
x2+bx+c,
得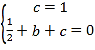 ,
,
解得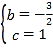 ,
,
∴抛物线的解折式为y=![]() x2-
x2-![]() x+1;
x+1;
∴抛物线的对称轴为x=![]() ,
,
∵B、C关于x=![]() 对称,
对称,
∴MC=MB,
要使|AM-MC|最大,即是使|AM-MB|最大,
由三角形两边之差小于第三边得,当A、B、M在同一直线上时|AM-MB|的值最大.
易知直线AB的解析式为y=-x+1
∴由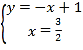 ,
,
得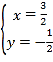 ,
,
∴M(![]() ,-
,-![]() ).
).
点睛: 本题综合考查了待定系数法求二次函数的解析式,二次函数的性质,直线和抛物线的交点,求两条线段和或差的最值,要考虑做其中一点关于所求的点在的直线的对称点.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】某服装超市购进单价为30元的童装若干件,物价部门规定其销售单价不低于每件30元,不高于每件60元.销售一段时间后发现:当销售单价为60元时,平均每月销售量为80件,而当销售单价每降低10元时,平均每月能多售出20件.同时,在销售过程中,每月还要支付其他费用450元.设销售单价为x元,平均月销售量为y件.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)当销售单价为多少元时,销售这种童装每月可获利1800元?
(3)当销售单价为多少元时,销售这种童装每月获得利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,AB=4.若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合).
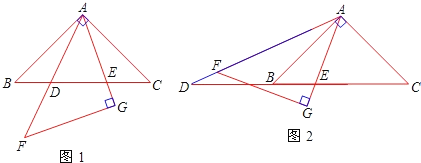
(1)求证:△ABE∽△DCA;
(2)若BE·CD=k(k为常数),求k的值;
(3)在旋转过程中,当△AFG旋转到如图2的位置时,AG与BC交于点E,AF的延长线与CB的延长线交于点D,那么(2)中k的值是否发生了变化?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
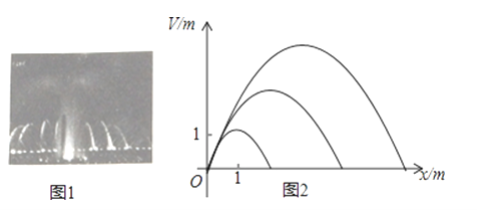
【题目】音乐喷泉(图1)可以使喷水造型随音乐的节奏起伏变化而变化.某种音乐喷泉形状如抛物线,设其出水口为原点,出水口离岸边18m,音乐变化时,抛物线的顶点在直线y=kx上变动,从而产生一组不同的抛物线(图2),这组抛物线的统一形式为y=ax2+bx.
(1)若已知k=1,且喷出的抛物线水线最大高度达3m,求此时a、b的值;
(2)若k=1,喷出的水恰好达到岸边,则此时喷出的抛物线水线最大高度是多少米?
(3)若k=3,a=﹣![]() ,则喷出的抛物线水线能否达到岸边?
,则喷出的抛物线水线能否达到岸边?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.

(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB的长度为2,AB所在直线上方存在点C,使得△ABC为等腰三角形,设△ABC的面积为S.当S=___________时,满足条件的点C恰有三个.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,D是弧![]() 的中点,过点D作DE⊥AC交AC的延长线于点E.
的中点,过点D作DE⊥AC交AC的延长线于点E.
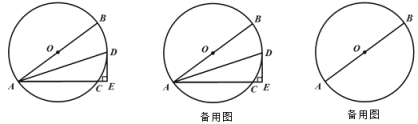
(1)求证:DE是⊙O的切线;
(2)当AB=10,AC=![]() 时,求弧
时,求弧![]() 的长;
的长;
(3)当AB=20时,直接写出△ABC面积最大时,点D到直径AB的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com