
【题目】如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,AB=4.若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合).
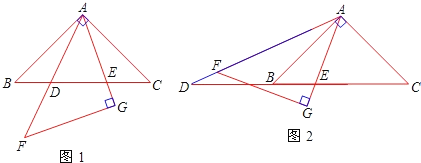
(1)求证:△ABE∽△DCA;
(2)若BE·CD=k(k为常数),求k的值;
(3)在旋转过程中,当△AFG旋转到如图2的位置时,AG与BC交于点E,AF的延长线与CB的延长线交于点D,那么(2)中k的值是否发生了变化?为什么?
【答案】(1)见解析;(2)k=16;(3)不变,理由见详解.
【解析】
(1)由于∠BAE=∠BAD+45°,∠CDA=∠BAD+45°,那么∠BAE=∠CDA,而∠B=∠C=45°,易证△ABE∽△DCA;
(2)由(1)知△ABE∽△DCA,可得![]() ,利用AB=CA=4,可求k的值;
,利用AB=CA=4,可求k的值;
(3)不变.由于∠BEA=∠EAC+45°,∠CAD=45°+∠EAC,易得∠BEA=∠CAD,而∠ABE=∠DCA=45°,可证△EBA∽△ACD,利用比例线段可求BECD=ABAC,而根据题意知AB=CA=4,从而可求k的值,可得不变的结论.
解:(1)∵三角形ABC和三角形AFG是两个全等的等腰直角三角形,
∴∠FAG=∠ACB=45°,∠B=∠C=45°,
∴∠BAE=∠BAD+45°,∠CDA=∠BAD+∠B =∠BAD+45°,
∴∠BAE=∠CDA,
∴△ABE∽△DCA,
(2)由(1)可知△ABE∽△DCA,
∴![]() ,
,
∴![]()
又∵三角形ABC是等腰直角三角形,AB=4,
∴AB=CA=4,
∴![]() ,
,
即![]() ,
,
(3)不变.
∵∠BEA=∠EAC+∠C =∠EAC+45°,
∠CAD=∠FAG +∠EAC=45°+∠EAC
∴∠BEA=∠CAD,
又∵∠ABE=∠DCA=45°,
∴△EBA∽△ACD,
∴![]() ,
,
∴![]() ,
,


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,F是⊙O上一点,连接FO、FB.C为![]() 中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
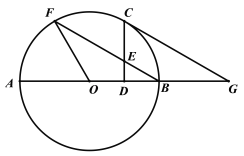
(1)求证:CG是⊙O的切线;
(2)若![]() BOF=120°,且CE=4,求⊙O的半径.
BOF=120°,且CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面图形S,点P、Q是S上任意两点,我们把线段PQ的长度的最大值称为平面图形S的“宽距”.例如,正方形的宽距等于它的对角线的长度.
(1)写出下列图形的宽距:
①半径为1的圆: ;
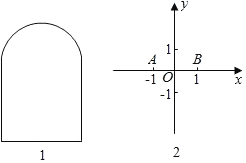
②如图1,上方是半径为1的半圆,下方是正方形的三条边的“窗户形“: ;
(2)如图2,在平面直角坐标系中,已知点A(﹣1,0)、B(1,0),C是坐标平面内的点,连接AB、BC、CA所形成的图形为S,记S的宽距为d.
①若d=2,求点C所在的区域的面积;
②若点C在⊙M上运动,⊙M的半径为1,圆心M在过点(0,2)且与y轴垂直的直线上.对于⊙M上任意点C,都有5≤d≤8,直接写出圆心M的横坐标x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() 的小球,它们的形状、大小、质地等完全相同.小强先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
的小球,它们的形状、大小、质地等完全相同.小强先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法或画树状图表示出(x,y)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(x,y)落在一次函数![]() 的图象上的概率;
的图象上的概率;
(3)求小强、小华各取一次小球所确定的数x、y满足![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
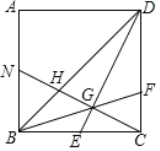
【题目】如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,交AB于N.下列结论:①DE=CN;②![]() ;③S△DEC=3S△BNH;④∠BGN=45°;⑤
;③S△DEC=3S△BNH;④∠BGN=45°;⑤![]() .其中正确结论的个数有( )
.其中正确结论的个数有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
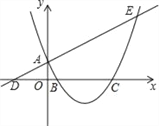
【题目】如图,已知直线y=![]() x+1与y轴交于点A,与x轴交于点D,抛物线y=
x+1与y轴交于点A,与x轴交于点D,抛物线y= ![]() x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标__________.
x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).在抛物线的对称轴上找一点M,使|AM﹣MC|的值最大,求出点M的坐标__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,∠ABC=90°,D是AB上一动点,连接CD,以CD为直径的⊙M交AC于点E,连接BM并延长交AC于点F,交⊙M于点G,连接BE.
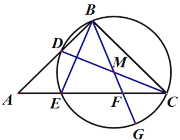
(1)求证:点B在⊙M上.
(2)当点D移动到使CD⊥BE时,求BC:BD的值.
(3)当点D到移动到使![]() 时,求证:AE+CF=EF.
时,求证:AE+CF=EF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com