
【题目】如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,交AB于N.下列结论:①DE=CN;②![]() ;③S△DEC=3S△BNH;④∠BGN=45°;⑤
;③S△DEC=3S△BNH;④∠BGN=45°;⑤![]() .其中正确结论的个数有( )
.其中正确结论的个数有( )
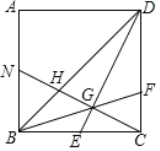
A.2个B.3个C.4个D.5个
【答案】D
【解析】
根据题目已知证明![]() 可判断①正确;证明
可判断①正确;证明![]() 可判断②正确;过H点作
可判断②正确;过H点作![]() ,利用
,利用![]() ,
,![]() 求解即可判断③正确;添加辅助线过B作BP⊥CN于P,BQ⊥DG,交DE的延长线于E,利用△BNC≌△CED,证得△BPN≌△BQE,即可判断④正确;连接N,E,设
求解即可判断③正确;添加辅助线过B作BP⊥CN于P,BQ⊥DG,交DE的延长线于E,利用△BNC≌△CED,证得△BPN≌△BQE,即可判断④正确;连接N,E,设![]() ,则
,则![]() ,
,![]() ,利用勾股定理求出CN,CE的长,然后根据
,利用勾股定理求出CN,CE的长,然后根据![]() 的面积求出GE,GN,再证
的面积求出GE,GN,再证![]() ,利用相似三角形对应边成比例,求出BG,BF的长,即可得⑤正确.
,利用相似三角形对应边成比例,求出BG,BF的长,即可得⑤正确.
解:①∵在正方形ABCD中,![]() ,
,![]() ,
,
∴![]()
![]()
即:![]()
∴![]() (ASA)
(ASA)
∴CN= DE,故①正确;
②∴在正方形ABCD中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,E为BC的中点, 四边形ABCD是正方形
,E为BC的中点, 四边形ABCD是正方形
∴![]() ,
,
∴![]() ,故②正确;
,故②正确;
③如下图示,过H点作![]() ,
,
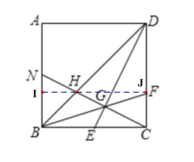
∴根据![]() ,有
,有![]() ,
,
则:![]()
∴![]() ,
,
![]()
即是:![]() ,故③正确 ;
,故③正确 ;
④过B作BP⊥CN于P,BQ⊥DG,交DE的延长线于E,
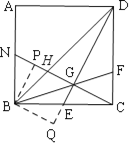
∴∠BPC=∠BQD=∠PGQ=90°,
∴四边形PBQG是矩形,
∴∠PBQ=90°,
∵∠ABC=90°,
∴∠NBP=∠QBE,
由①得:△BNC≌△CED,
∴EC=BN,
∵E是BC的中点,
∴BE=EC,
∴BE=BN,
∵∠BPN=∠BQE=90°,
∴△BPN≌△BQE,
∴BP=BQ,
∴四边形PBQG是正方形,
∴∠BGE=45°,故④正确;
⑤如图示,连接N,E
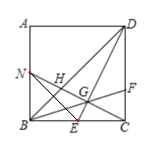
设![]() ,则
,则![]() ,
,![]() ,
,
∵CG⊥DE,![]()
∴![]() ,
,
![]() ,
,
由![]() 的面积可得:
的面积可得:![]()
化简得:![]() ,
,
∴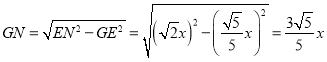 ,
,
则有:![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴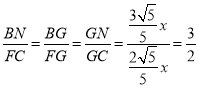 ,
,
∴![]() ,
,
则![]() ,
,
![]() ,
,
并∵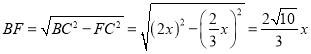
∴![]()
∴![]() ,故⑤正确.
,故⑤正确.
综上所述,故选:D.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】“绿水青山,就是金山银山”,为了改善生态环境,某县政府准备对境内河流进行清淤、疏通河道,同时在人群密集区沿河流修建滨河步道,打造生态湿地公园.
(1)2018年11月至12月,一期工程原计划疏通河道和修建滨河步道里程数共计20千米,其中修建滨河步道里程数是疏通河道里程数的![]() 倍,那么,原计划修建滨河步道多少千米?
倍,那么,原计划修建滨河步道多少千米?
(2)至2018年12月底,一期工程顺利按原计划完成总共耗资840万元,其中疏通河道工程共耗资600万元;2019年二期工程开工后,疏通河道每千米工程费用较一期降低2.5a%,里程数较一期增加3a%;修建滨河步道每千米工程费用较一期上涨2.5a%,里程数较一期增加5a%,经测算,二期工程总费用将比一期增加2a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2x+m.
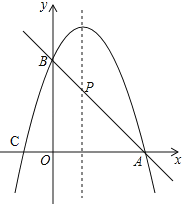
(1)如果抛物线过点A(3,0),与y轴交于点B,求抛物线的解析式及点B、C的坐标;
(2)如图,直线AB与这条抛物线的对称轴交于点P,求直线AB的表达式和点P的坐标.
(3)该抛物线有一点D(x,y),使得S△ABC=S△ACD,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC的垂直平分线EF交∠ABC的平分线BD于E,如果∠BAC=60°,∠ACE=24°,那么∠BCE的大小是( )

A. 24° B. 30° C. 32° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:四边形ABCD中,E、F、G、H分别为各边的中点,顺次连接E、F、G、H,把四边形EFGH称为中点四边形.连接AC、BD,容易证明:中点四边形EFGH一定是平行四边形.
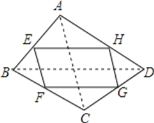
(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:当四边形ABCD的对角线满足AC=BD时,四边形EFGH为菱形.当四边形ABCD的对角线满足 时,四边形EFGH为矩形;当四边形ABCD的对角线满足 时,四边形EFGH为正方形;
(2)探索三角形AEH、三角形CFG与四边形ABCD的面积之间的等量关系,请写出你发现的结论,并加以证明;
(3)如果四边形ABCD的面积为2,那么中点四边形EFGH的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,AB=4.若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合).
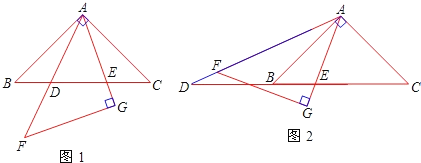
(1)求证:△ABE∽△DCA;
(2)若BE·CD=k(k为常数),求k的值;
(3)在旋转过程中,当△AFG旋转到如图2的位置时,AG与BC交于点E,AF的延长线与CB的延长线交于点D,那么(2)中k的值是否发生了变化?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.

(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB、BC是半径为![]() 的⊙O内的两条弦,且AB=6,BC=8.(1)若∠ABC=90°,则
的⊙O内的两条弦,且AB=6,BC=8.(1)若∠ABC=90°,则![]() =________;(2)若∠ABC=120°,则
=________;(2)若∠ABC=120°,则![]() =______.
=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com