
【题目】“绿水青山,就是金山银山”,为了改善生态环境,某县政府准备对境内河流进行清淤、疏通河道,同时在人群密集区沿河流修建滨河步道,打造生态湿地公园.
(1)2018年11月至12月,一期工程原计划疏通河道和修建滨河步道里程数共计20千米,其中修建滨河步道里程数是疏通河道里程数的![]() 倍,那么,原计划修建滨河步道多少千米?
倍,那么,原计划修建滨河步道多少千米?
(2)至2018年12月底,一期工程顺利按原计划完成总共耗资840万元,其中疏通河道工程共耗资600万元;2019年二期工程开工后,疏通河道每千米工程费用较一期降低2.5a%,里程数较一期增加3a%;修建滨河步道每千米工程费用较一期上涨2.5a%,里程数较一期增加5a%,经测算,二期工程总费用将比一期增加2a%,求a的值.
【答案】(1)原计划修建滨河步道8千米;(2)a的值是28.
【解析】
(1)根据修建滨河步道里程数是疏通河道里程数的![]() 倍,列方程即可得出结论;
倍,列方程即可得出结论;
(2)先根据一期工程修建滨河步道里程数是疏通河道里程数与工程费用计算出每千米修建滨河步道与疏通河道的工程费,然后根据题意列方程,并利用换元法解方程即可得出结论.
(1)设原计划修建滨河步道x千米,
根据题意,得![]() .解这个方程,得
.解这个方程,得![]() .
.
答:原计划修建滨河步道8千米
(2)根据题意,
一期工程疏通河道里程数:![]() (千米).
(千米).
一期工程疏通河道费用:![]() (万元/千米).
(万元/千米).
一期工程修建滨河步道费用:![]() (万元/千米)
(万元/千米)
![]()
令![]() ,原方程可化为
,原方程可化为
![]() ,
,
整理这个方程,得![]() .
.
解这个方程,得![]() ,
,![]() .
.
∴![]() (舍去),
(舍去),![]() .∴
.∴![]() .
.
答:a的值是28.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2﹣4ax﹣5(a>0).
(1)当a=1时,求抛物线与x轴的交点坐标及对称轴;
(2)①试说明无论a为何值,抛物线C1一定经过两个定点,并求出这两个定点的坐标;
②将抛物线C1沿这两个定点所在直线翻折,得到抛物线C2,直接写出C2的表达式;
(3)若(2)中抛物线C2的顶点到x轴的距离为2,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,在下列结论中,不正确的是( )
,在下列结论中,不正确的是( )
A.图象必经过点(4,![]() )
)
B.图象过第一、三象限
C.若x<-1,则y>-6
D.点 ![]()
![]() 、
、![]()
![]() 是图象上的两点,
是图象上的两点, ![]() ,则
,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.
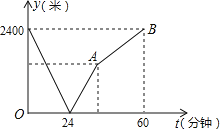
(1)根据图象信息,当t= 分钟时甲乙两人相遇,甲的速度为 米/分钟,乙的速度为 米/分钟;
(2)图中点A的坐标为 ;
(3)求线段AB所直线的函数表达式;
(4)在整个过程中,何时两人相距400米?
查看答案和解析>>
科目:初中数学 来源: 题型:
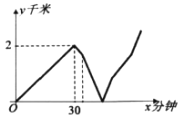
【题目】周末小明匀速步行赶往学校参加学校组织的植树活动,小明从家出发30分钟后,忽然想起没有带植树工具,于是马上掉头往回走行走速度比之前提高了1千米/时(仍保持匀速步行),同时小明打电话给爸爸,请爸爸帮他把植树工具送过来,从小明开始打电话到爸爸出门一共用了4分钟,爸爸的行走速度与此时小明的行走速度相同,两人相遇后,小明立即赶往学校,爸爸则转身回家,两人速度均保持不变,爸爸在回家途中用了10分钟吃早餐,然后立即回家,当爸爸到家时小明刚好到达学校.爸爸和小明相距的路程y(千米)与小明从家出发的时间x(分钟)之间的关系如图所示,求今天早上小明从家到学校途中行走的总路程是________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
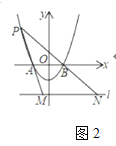
【题目】如图,经过![]() 和
和![]() 两点的抛物线
两点的抛物线![]() 交
交![]() 轴于
轴于![]() 两点,
两点,![]() 是抛物线上一动点,平行于
是抛物线上一动点,平行于![]() 轴的直线
轴的直线![]() 经过点
经过点![]() .
.
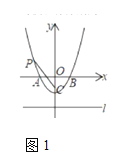
(1)求抛物线的解析式;
(2)如图1,![]() 轴上有点
轴上有点![]() 连接
连接![]() ,设点
,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.![]() .小明在探究
.小明在探究![]() 的值的过程中,是这样思考的:当
的值的过程中,是这样思考的:当![]() 是抛物线的顶点时,计算
是抛物线的顶点时,计算![]() 的值;当
的值;当![]() 不是抛物线的顶点时,猜想
不是抛物线的顶点时,猜想![]() 是一个定值.请你直接写出
是一个定值.请你直接写出![]() 的值,并证明小明的猜想.
的值,并证明小明的猜想.
(3)如图2,点![]() 在第二象限,分别连接
在第二象限,分别连接![]() 、
、![]() ,并延长交直线
,并延长交直线![]() 于
于![]() 两点.若
两点.若![]() 两点的横坐标分别为
两点的横坐标分别为![]() ,试探究
,试探究![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作d(M).
(1)已知点E(0,4),
①直接写出d(点E)的值;
②直线y=kx+4(k≠0)与x轴交于点F,当d(线段EF)取最小值时,求k的取值范围;
(2)⊙T的圆心为T(7,t),半径为1.若d(⊙T)<11,请直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
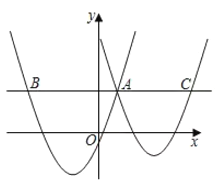
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 交于点A.过点A作
交于点A.过点A作![]() 轴的垂线,分别交两条抛物线于点B、C(点B在点A左侧,点C在点A右侧),则线段BC的长为____.
轴的垂线,分别交两条抛物线于点B、C(点B在点A左侧,点C在点A右侧),则线段BC的长为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com