
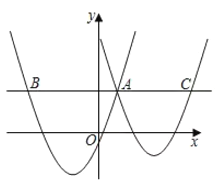
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 交于点A.过点A作
交于点A.过点A作![]() 轴的垂线,分别交两条抛物线于点B、C(点B在点A左侧,点C在点A右侧),则线段BC的长为____.
轴的垂线,分别交两条抛物线于点B、C(点B在点A左侧,点C在点A右侧),则线段BC的长为____.
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】“绿水青山,就是金山银山”,为了改善生态环境,某县政府准备对境内河流进行清淤、疏通河道,同时在人群密集区沿河流修建滨河步道,打造生态湿地公园.
(1)2018年11月至12月,一期工程原计划疏通河道和修建滨河步道里程数共计20千米,其中修建滨河步道里程数是疏通河道里程数的![]() 倍,那么,原计划修建滨河步道多少千米?
倍,那么,原计划修建滨河步道多少千米?
(2)至2018年12月底,一期工程顺利按原计划完成总共耗资840万元,其中疏通河道工程共耗资600万元;2019年二期工程开工后,疏通河道每千米工程费用较一期降低2.5a%,里程数较一期增加3a%;修建滨河步道每千米工程费用较一期上涨2.5a%,里程数较一期增加5a%,经测算,二期工程总费用将比一期增加2a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣2mx﹣3,有下列说法:
①它的图象与x轴有两个公共点;
②如果当x≤1时y随x的增大而减小,则m=1;
③如果将它的图象向左平移3个单位后过原点,则m=﹣1;
④如果当x=4时的函数值与x=2008时的函数值相等,则当x=2012时的函数值为﹣3.
其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
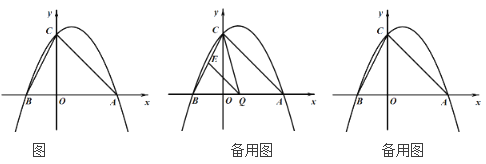
【题目】如图已知抛物线与![]() 轴交于点C(0,4),与
轴交于点C(0,4),与![]() 轴交于A(
轴交于A(![]() ,0)、B(
,0)、B(![]() ,0),其中
,0),其中![]() ,
,![]() 为方程
为方程![]() 的两个根.
的两个根.
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连结CQ,设Q(![]() ,0),△CQE的面积为
,0),△CQE的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式及△CQE的面积的最大值;
的函数关系式及△CQE的面积的最大值;
(3)点M的坐标为(2,0),问:在直线AC上,是否存在点F,使得△OMF是等腰三角形?若存在,请求出点F的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
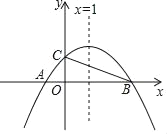
【题目】如图,已知抛物线y=ax2+bx+1与x轴相交于点A,B,与y轴相交于点C,点A的坐标为(﹣1,0),对称轴为直线x=1.
(1)求点B的坐标及抛物线的解析式;
(2)在直线BC上方的抛物线上有一点P,使△PBC的面积为1,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
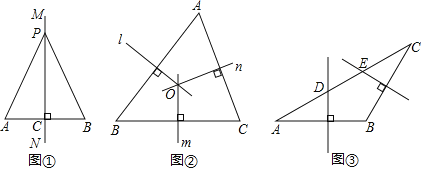
【题目】教材呈现:下图是华师版八年级上册数学教材第94页的部分内容.
线段垂直平分线
我们已知知道线段是轴对称图形,线段的垂直一部分线是线段的对称轴,如图直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,![]() 是
是![]() 上任一点,连结
上任一点,连结![]() 、
、![]() ,将线段
,将线段![]() 与直线
与直线![]() 对称,我们发现
对称,我们发现![]() 与
与![]() 完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
已知:如图,![]() ,垂足为点
,垂足为点![]() ,
,![]() ,点
,点![]() 是直线
是直线![]() 上的任意一点.
上的任意一点.
求证:![]() .
.
图中的两个直角三角形![]() 和
和![]() ,只要证明这两个三角形全等,便可证明
,只要证明这两个三角形全等,便可证明![]() (请写出完整的证明过程)
(请写出完整的证明过程)
请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程,定理应用.
(1)如图②,在![]() 中,直线
中,直线![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 、
、![]() 的垂直平分线.
的垂直平分线.
求证:直线![]() 、
、![]() 、
、![]() 交于点.
交于点.
(2)如图③,在![]() 中,
中,![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为_______.
的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
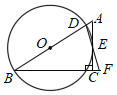
【题目】如图,在Rt△ABC中,∠ACB=90°,点D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连接DE并延长DE交BC的延长线于点F.
(1)求证:BD=BF;
(2)填空:
①若⊙O的半径为5,tanB=![]() ,则CF= ;
,则CF= ;
②若⊙O与BF相交于点H,当∠B的度数为 时,四边形OBHE为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万kg与3.6万kg,现假定该养殖场蛋鸡产蛋量的月增长率相同.
(1)求该养殖场蛋鸡产蛋量的月平均增长率;
(2)假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万kg.如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=![]() 的图像与
的图像与![]() 轴的一个交点为A(-1,0),另一个交点为B,与
轴的一个交点为A(-1,0),另一个交点为B,与![]() 轴交于点C(0,﹣3),顶点为D.
轴交于点C(0,﹣3),顶点为D.
(1)求二次函数的解析式和点D的坐标;
(2)若点M是抛物线在![]() 轴下方图像上的一动点,过点M作MN∥
轴下方图像上的一动点,过点M作MN∥![]() 轴交线段BC于点N,当MN取最大值时,点M 的坐标;
轴交线段BC于点N,当MN取最大值时,点M 的坐标;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点D落在x轴上,原抛物线上一点P平移后的对应点为Q,如果∠OQP=∠OPQ,试求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com