
【题目】教材呈现:下图是华师版八年级上册数学教材第94页的部分内容.
线段垂直平分线
我们已知知道线段是轴对称图形,线段的垂直一部分线是线段的对称轴,如图直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,![]() 是
是![]() 上任一点,连结
上任一点,连结![]() 、
、![]() ,将线段
,将线段![]() 与直线
与直线![]() 对称,我们发现
对称,我们发现![]() 与
与![]() 完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
已知:如图,![]() ,垂足为点
,垂足为点![]() ,
,![]() ,点
,点![]() 是直线
是直线![]() 上的任意一点.
上的任意一点.
求证:![]() .
.
图中的两个直角三角形![]() 和
和![]() ,只要证明这两个三角形全等,便可证明
,只要证明这两个三角形全等,便可证明![]() (请写出完整的证明过程)
(请写出完整的证明过程)
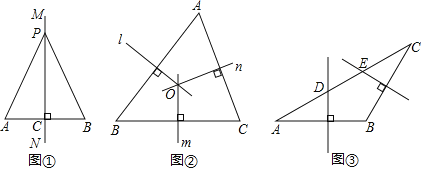
请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程,定理应用.
(1)如图②,在![]() 中,直线
中,直线![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 、
、![]() 的垂直平分线.
的垂直平分线.
求证:直线![]() 、
、![]() 、
、![]() 交于点.
交于点.
(2)如图③,在![]() 中,
中,![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为_______.
的长为_______.
【答案】教材呈现:详见解析;定理应用:(1)详见解析;(2)6.
【解析】
教材呈现: ![]()
![]() 得到
得到![]() ,从而
,从而![]()
定理应用:(1)连结![]() 、
、![]() 、
、![]() .设直线
.设直线![]() 、
、![]() 交于点
交于点![]() .因为直线
.因为直线![]() 是边
是边![]() 的垂直平分线,所以
的垂直平分线,所以![]() 又因直线
又因直线![]() 是边
是边![]() 的垂直平分线,
的垂直平分线,![]() 得到
得到![]() 点
点![]() 在边
在边![]() 的垂直平分线
的垂直平分线![]() 上.得到直线
上.得到直线![]() 、
、![]() 、
、![]() 交于点
交于点![]() . (2)
. (2)
连接BD,BF,易知AD=DB,BE=EC;又因为∠A=∠C=30°,得到∠DBE=60°,所以∠ABD=30°,得到∠BDE=60°,所以△BED为等边三角形,所以DE=![]() AC=6
AC=6
教材呈现:
![]()
![]() ,
,
![]()
![]()
又![]()
![]()
![]()
![]() .
.
![]()
![]()
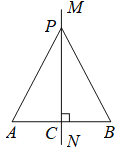
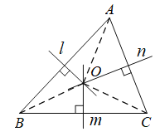
图① 图②
定理应用:
(1)连结![]() 、
、![]() 、
、![]() .
.
设直线![]() 、
、![]() 交于点
交于点![]() .
.
![]() 直线
直线![]() 是边
是边![]() 的垂直平分线,
的垂直平分线,
![]()
![]()
又![]() 直线
直线![]() 是边
是边![]() 的垂直平分线,
的垂直平分线,
![]()
![]()
![]()
![]()
![]() 在边
在边![]() 的垂直平分线
的垂直平分线![]() 上.
上.
![]() 直线
直线![]() 、
、![]() 、
、![]() 交于点
交于点![]() .
.
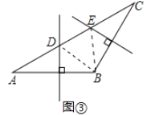
(2)如图3,连接BD,BF
由第一问可知,AD=DB,BE=EC,∠A=∠DBA,∠C=∠CBE
∵AB=AC
∴∠A=∠C
∵∠ABC=120°
∴∠A=∠C=30°
∴∠A=∠DBA=∠C=∠CBE=30°
∴∠BDE=∠A+∠ABD=60°,∠DBE=∠ABC-∠ABD-∠EBC=60°
∴△DBE是等边三角形
∴DB=BE=DE
∴AD=DE=EC
∴DE=![]() AC=6
AC=6


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为全面贯彻党的教育方针,坚持“健康第一”的教育理念,促进学生健康成长,提高体质健康水平,成都市调整体育中考实施方案:分值增加至60,男1000米(女800米)必考,足球、篮球、排球“三选一”…,从2019年秋季新入学的七年级起开始实施.某中学为了解七年级学生对三大球类运动的喜爱情况,从七年级学生中随机抽取部分学生进行调查问卷,通过分析整理绘制了如下两幅统计图.请根据两幅统计图中的信息回答下列问题:
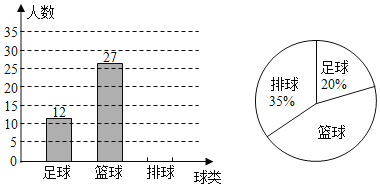
(1)求参与调查的学生中,喜爱排球运动的学生人数,并补全条形图;
(2)若该中学七年级共有400名学生,请你估计该中学七年级学生中喜爱篮球运动的学生有多少名?
(3)若从喜爱足球运动的2名男生和2名女生中随机抽取2名学生,确定为该校足球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
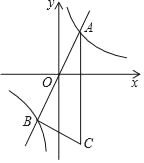
【题目】如图,反比例函数的图象与正比例函数y=2x的图象相交于A(1,a),B两点,点C在第四象限,CA∥y轴,∠ABC=90°
(1)求反比例函数的解析式及点B的坐标;
(2)求tanC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
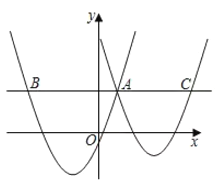
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 交于点A.过点A作
交于点A.过点A作![]() 轴的垂线,分别交两条抛物线于点B、C(点B在点A左侧,点C在点A右侧),则线段BC的长为____.
轴的垂线,分别交两条抛物线于点B、C(点B在点A左侧,点C在点A右侧),则线段BC的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
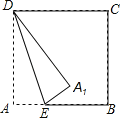
【题目】如图,已知正方形ABCD,边长为8,E是AB边上的一点,连接DE,将△DAE沿DE所在直线折叠,使点A的对应点A1落在正方形的边CD或BC的垂直平分线上,则AE的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
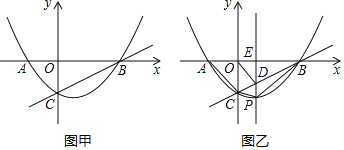
【题目】如图甲,抛物线y=ax2+bx﹣1经过A(﹣1,0),B(2,0)两点,交y轴于点C.
(1)求抛物线的表达式和直线BC的表达式.
(2)如图乙,点P为在第四象限内抛物线上的一个动点,过点P作x轴的垂线PE交直线BC于点D.
①在点P运动过程中,四边形ACPB的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由.
②是否存在点P使得以点O,C,D为顶点的三角形是等腰三角形?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点A(3,1)与点B(0,4).
经过点A(3,1)与点B(0,4).

(1)求该抛物线的解析式及顶点坐标;
(2)在第三象限内的抛物线上有一点P,使得PA⊥AB,求点P的坐标;
(3)若点C(![]() ,
,![]() )在该抛物线上,当
)在该抛物线上,当![]() ≤
≤![]() ≤3时,1≤
≤3时,1≤![]() ≤5,请确定
≤5,请确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
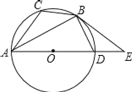
⑴求证:BE是⊙O的切线;
⑵若BC=![]() ,AC=5,求圆的直径AD的长.
,AC=5,求圆的直径AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com