
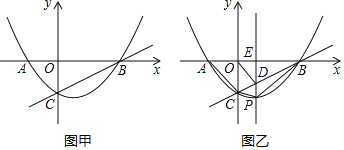
ЁОЬтФПЁПШчЭММзЃЌХзЮяЯпyЃНax2+bxЉ1ОЙ§AЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌНЛyжсгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНКЭжБЯпBCЕФБэДяЪНЃЎ
ЃЈ2ЃЉШчЭМввЃЌЕуPЮЊдкЕкЫФЯѓЯоФкХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпPEНЛжБЯпBCгкЕуDЃЎ
ЂйдкЕуPдЫЖЏЙ§ГЬжаЃЌЫФБпаЮACPBЕФУцЛ§ЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧѓГіетИізюДѓжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЂкЪЧЗёДцдкЕуPЪЙЕУвдЕуOЃЌCЃЌDЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіТњзуЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉХзЮяЯпЕФБэДяЪНЮЊЃК![]() ЃЌжБЯпBCЕФБэДяЪНЮЊЃКyЃН
ЃЌжБЯпBCЕФБэДяЪНЮЊЃКyЃН![]() xЉ1ЃЛЃЈ2ЃЉЂйДцдкЃЌзюДѓжЕЮЊ2ЃЛЂкЃЈ
xЉ1ЃЛЃЈ2ЃЉЂйДцдкЃЌзюДѓжЕЮЊ2ЃЛЂкЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ1ЃЌЉ1ЃЉЛђЃЈ
ЃЉЛђЃЈ1ЃЌЉ1ЃЉЛђЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
(1) ЩшЖўДЮКЏЪ§ЕФБэДяЪНЮЊЃКyЃНaЃЈx+1ЃЉЃЈxЉ2ЃЉЃНax2ЉaxЉ2aЃЌМДЃКЉ2aЃНЉ1ЃЌМДПЩЧѓНтЃЛгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіжБЯпBCЕФБэДяЪНЃЎ
(2) ЂйSЫФБпаЮACPBЃНSЁїABC+SЁїBCPЃН![]() ЁСABЁСOC+
ЁСABЁСOC+![]() ЁСPDЁСOBЃЌМДПЩЧѓНтЃЛ
ЁСPDЁСOBЃЌМДПЩЧѓНтЃЛ
ЂкЗжCDЃНOCЁЂCDЃНODЁЂOCЃНODШ§жжЧщПіЗжБ№ЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉЖўДЮКЏЪ§ЕФБэДяЪНЮЊЃКyЃНaЃЈx+1ЃЉЃЈxЉ2ЃЉЃНax2ЉaxЉ2aЃЌ
МДЃКЉ2aЃНЉ1ЃЌНтЕУЃКaЃН![]() ЃЌ
ЃЌ
ЙЪХзЮяЯпЕФБэДяЪНЮЊЃК![]() ЃЌЕуCЃЈ0ЃЌЉ1ЃЉЃЌ
ЃЌЕуCЃЈ0ЃЌЉ1ЃЉЃЌ
дђжБЯпBCЕФБэДяЪНЮЊЃКyЃНkxЉ1ЃЌ
НЋЕуBЕФзјБъДњШыЩЯЪНЕУЃК0ЃН2kЉ1ЃЌНтЕУЃКkЃН![]() ЃЌ
ЃЌ
ЙЪжБЯпBCЕФБэДяЪНЮЊЃКyЃН![]() xЉ1ЃЛ
xЉ1ЃЛ
ЃЈ2ЃЉЂйЩшЕуPЃЈxЃЌ![]() x2Љ
x2Љ![]() xЉ1ЃЉЃЌдђЕуDЃЈxЃЌ
xЉ1ЃЉЃЌдђЕуDЃЈxЃЌ![]() xЉ1ЃЉЃЌ
xЉ1ЃЉЃЌ
SЫФБпаЮACPBЃНSЁїABC+SЁїBCPЃН![]() ЁСABЁСOC+
ЁСABЁСOC+![]() ЁСPDЁСOB
ЁСPDЁСOB
ЃН![]() ЁС3ЁС1+
ЁС3ЁС1+![]() ЁС2ЃЈ
ЁС2ЃЈ![]() xЉ1Љ
xЉ1Љ![]() x2+
x2+![]() x+1ЃЉЃНЉ
x+1ЃЉЃНЉ![]() x2+x+
x2+x+![]() ЃЌ
ЃЌ
ЁпЉ![]() 0ЃЌЙЪSгазюДѓжЕЃЌЕБxЃН1ЪБЃЌSзюДѓжЕЮЊ2ЃЛ
0ЃЌЙЪSгазюДѓжЕЃЌЕБxЃН1ЪБЃЌSзюДѓжЕЮЊ2ЃЛ
ЂкЩшЕуDзјБъЮЊЃЈmЃЌ![]() mЉ1ЃЉЃЌ
mЉ1ЃЉЃЌ
дђCD2ЃНm2+![]() m2ЃЌOC2ЃН1ЃЌDO2ЃНm2+ЃЈ
m2ЃЌOC2ЃН1ЃЌDO2ЃНm2+ЃЈ![]() mЉ1ЃЉ2ЃН
mЉ1ЃЉ2ЃН![]() m2Љm+1ЃЌ
m2Љm+1ЃЌ
ЕБCDЃНOCЪБЃЌm2+![]() m2ЃН1ЃЌНтЕУЃКmЃН
m2ЃН1ЃЌНтЕУЃКmЃН![]() ЃЌ
ЃЌ
ЭЌРэПЩЕУЃК
ЕБCDЃНODЪБЃЌmЃН1ЃЌ
ЕБOCЃНODЪБЃЌmЃН![]() ЃЌ
ЃЌ
дђЕуPзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ1ЃЌЉ1ЃЉЛђЃЈ
ЃЉЛђЃЈ1ЃЌЉ1ЃЉЛђЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЎ
ЃЉЃЎ


 УћЪІЕМКНЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ
УћЪІЕМКНЕЅдЊЦкФЉГхДЬ100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЪЧМзЁЂввСНаЃФаЁЂХЎЩњШЫЪ§ЕФЭГМЦЭМЃЎ

ИљОнЭГМЦЭМЛиД№ЮЪЬтЃК
ЃЈ1ЃЉШєМзаЃФаЩњШЫЪ§ЮЊ273ШЫЃЌЧѓИУаЃХЎЩњШЫЪ§ЃЛ
ЃЈ2ЃЉЗНЗНЭЌбЇЫЕЃКЁАвђЮЊМзаЃХЎЩњШЫЪ§еМШЋаЃШЫЪ§ЕФ40%ЃЌЖјвваЃХЎЩњШЫЪ§еМШЋаЃШЫЪ§ЕФ45%ЃЌЫљвдМзаЃЕФХЎЩњШЫЪ§БШвваЃХЎЩњШЫЪ§ЩйЁБЃЌФуШЯЮЊЗНЗНЭЌбЇЫЕЕФЖдТ№ЃПЮЊЪВУДЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМвбжЊХзЮяЯпгы![]() жсНЛгкЕуC(0ЃЌ4)ЃЌгы
жсНЛгкЕуC(0ЃЌ4)ЃЌгы![]() жсНЛгкA(
жсНЛгкA(![]() ЃЌ0)ЁЂB(
ЃЌ0)ЁЂB(![]() ЃЌ0)ЃЌЦфжа
ЃЌ0)ЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЮЊЗНГЬ
ЮЊЗНГЬ![]() ЕФСНИіИљЃЎ
ЕФСНИіИљЃЎ
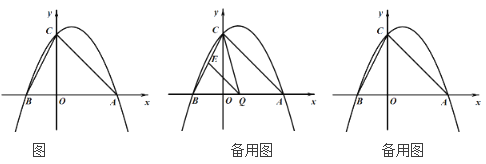
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуQЪЧЯпЖЮABЩЯЕФЖЏЕуЃЌЙ§ЕуQзїQEЁЮACЃЌНЛBCгкЕуEЃЌСЌНсCQЃЌЩшQ(![]() ЃЌ0)ЃЌЁїCQEЕФУцЛ§ЮЊ
ЃЌ0)ЃЌЁїCQEЕФУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНМАЁїCQEЕФУцЛ§ЕФзюДѓжЕЃЛ
ЕФКЏЪ§ЙиЯЕЪНМАЁїCQEЕФУцЛ§ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉЕуMЕФзјБъЮЊ(2ЃЌ0)ЃЌЮЪЃКдкжБЯпACЩЯЃЌЪЧЗёДцдкЕуFЃЌЪЙЕУЁїOMFЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕуFЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЬВФГЪЯжЃКЯТЭМЪЧЛЊЪІАцАЫФъМЖЩЯВсЪ§бЇНЬВФЕк94вГЕФВПЗжФкШн.
ЯпЖЮДЙжБЦНЗжЯп
ЮвУЧвбжЊжЊЕРЯпЖЮЪЧжсЖдГЦЭМаЮЃЌЯпЖЮЕФДЙжБвЛВПЗжЯпЪЧЯпЖЮЕФЖдГЦжсЃЌШчЭМжБЯп![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФДЙжБЦНЗжЯпЃЌ
ЕФДЙжБЦНЗжЯпЃЌ![]() ЪЧ
ЪЧ![]() ЩЯШЮвЛЕуЃЌСЌНс
ЩЯШЮвЛЕуЃЌСЌНс![]() ЁЂ
ЁЂ![]() ЃЌНЋЯпЖЮ
ЃЌНЋЯпЖЮ![]() гыжБЯп
гыжБЯп![]() ЖдГЦЃЌЮвУЧЗЂЯж
ЖдГЦЃЌЮвУЧЗЂЯж![]() гы
гы![]() ЭъШЋжиКЯЃЌгЩДЫЖМгаЃКЯпЖЮДЙжБЦНЗжЯпЕФаджЪЖЈРэЃЌЯпЖЮДЙжБЦНЗжЯпЩЯЕФЕуЕНЯпЖЮЕФОрРыЯрЕШ.
ЭъШЋжиКЯЃЌгЩДЫЖМгаЃКЯпЖЮДЙжБЦНЗжЯпЕФаджЪЖЈРэЃЌЯпЖЮДЙжБЦНЗжЯпЩЯЕФЕуЕНЯпЖЮЕФОрРыЯрЕШ.
вбжЊЃКШчЭМЃЌ![]() ЃЌДЙзуЮЊЕу
ЃЌДЙзуЮЊЕу![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЕФШЮвтвЛЕу.
ЩЯЕФШЮвтвЛЕу.
ЧѓжЄЃК![]() .
.
ЭМжаЕФСНИіжБНЧШ§НЧаЮ![]() КЭ
КЭ![]() ЃЌжЛвЊжЄУїетСНИіШ§НЧаЮШЋЕШЃЌБуПЩжЄУї
ЃЌжЛвЊжЄУїетСНИіШ§НЧаЮШЋЕШЃЌБуПЩжЄУї![]() ЃЈЧыаДГіЭъећЕФжЄУїЙ§ГЬЃЉ
ЃЈЧыаДГіЭъећЕФжЄУїЙ§ГЬЃЉ
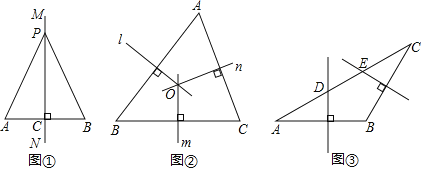
ЧыИљОнНЬВФжаЕФЗжЮіЃЌНсКЯЭМЂйЃЌаДГіЁАЯпЖЮДЙжБЦНЗжЯпЕФаджЪЖЈРэЁБЭъећЕФжЄУїЙ§ГЬЃЌЖЈРэгІгУ.
ЃЈ1ЃЉШчЭМЂкЃЌдк![]() жаЃЌжБЯп
жаЃЌжБЯп![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧБп
ЗжБ№ЪЧБп![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЕФДЙжБЦНЗжЯп.
ЕФДЙжБЦНЗжЯп.
ЧѓжЄЃКжБЯп![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() НЛгкЕу.
НЛгкЕу.
ЃЈ2ЃЉШчЭМЂлЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌБп
ЃЌБп![]() ЕФДЙжБЦНЗжЯпНЛ
ЕФДЙжБЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌБп
ЃЌБп![]() ЕФДЙжБЦНЗжЯпНЛ
ЕФДЙжБЦНЗжЯпНЛ![]() гкЕу
гкЕу![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЮЊ_______.
ЕФГЄЮЊ_______.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
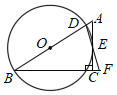
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌЕуDЪЧABБпЩЯвЛЕуЃЌвдBDЮЊжБОЖЕФЁбOгыБпACЯрЧагкЕуEЃЌСЌНгDEВЂбгГЄDEНЛBCЕФбгГЄЯпгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКBDЃНBFЃЛ
ЃЈ2ЃЉЬюПеЃК
ЂйШєЁбOЕФАыОЖЮЊ5ЃЌtanBЃН![]() ЃЌдђCFЃНЁЁ ЁЁЃЛ
ЃЌдђCFЃНЁЁ ЁЁЃЛ
ЂкШєЁбOгыBFЯрНЛгкЕуHЃЌЕБЁЯBЕФЖШЪ§ЮЊЁЁ ЁЁЪБЃЌЫФБпаЮOBHEЮЊСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃзщжЏШЋаЃбЇЩњНјааСЫвЛДЮЁАЩчЛсжївхКЫаФМлжЕЙлЁБжЊЪЖОКШќЃЌШќКѓЫцЛњГщШЁСЫИїФъМЖВПЗжбЇЩњГЩМЈНјааЭГМЦЃЌжЦзїШчЯТЦЕЪ§ЗжВМБэКЭЦЕЪ§ЗжВМжБЗНЭМЃЎЧыИљОнЭМБэжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЗжЪ§ЖЮЃЈ | ЦЕЪ§ | ЦЕТЪ |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
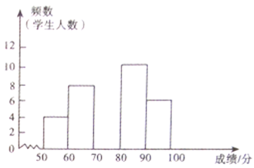
ЃЈ1ЃЉЧыЧѓГіИУаЃЫцЛњГщШЁСЫ____бЇЩњГЩМЈНјааЭГМЦЃЛ
ЃЈ2ЃЉБэжа![]() ____ЃЌ
____ЃЌ![]() ____ЃЌВЂВЙШЋжБЗНЭМЃЛ
____ЃЌВЂВЙШЋжБЗНЭМЃЛ
ЃЈ3ЃЉШєгУЩШаЮЭГМЦЭМУшЪіДЫГЩМЈЭГМЦЗжВМЧщПіЃЌдђЗжЪ§ЖЮ![]() ЖдгІЩШаЮЕФдВаФНЧЖШЪ§ЪЧ___
ЖдгІЩШаЮЕФдВаФНЧЖШЪ§ЪЧ___![]() ЃЛ
ЃЛ
ЃЈ4ЃЉШєИУаЃЙВгабЇЩњ8000ШЫЃЌЧыЙРМЦИУаЃЗжЪ§дк![]() ЕФбЇЩњгаЖрЩйШЫЃП
ЕФбЇЩњгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбјжГГЁЮЊСЫЯьгІЕГжабыЕФЗіЦЖеўВпЃЌНёФъЦ№ВЩгУЁАГЁФк+ХЉЛЇЁБбјжГФЃЪНЃЌЭЌЪБМгЧПЖдЕАМІЕФПЦбЇЙмРэЃЌЕАМІЕФВњЕАТЪВЛЖЯЬсИпЃЌШ§дТЗнКЭЮхдТЗнЕФВњЕАСПЗжБ№ЪЧ2.5Эђkgгы3.6ЭђkgЃЌЯжМйЖЈИУбјжГГЁЕАМІВњЕАСПЕФдТдіГЄТЪЯрЭЌЃЎ
ЃЈ1ЃЉЧѓИУбјжГГЁЕАМІВњЕАСПЕФдТЦНОљдіГЄТЪЃЛ
ЃЈ2ЃЉМйЖЈЕБдТВњЕФМІЕАЕБдТдкИїЯњЪлЕуШЋВПЯњЪлГіШЅЃЌЧвУПИіЯњЪлЕуУПдТЦНОљЯњЪлСПзюЖрЮЊ0.32ЭђkgЃЎШчЙћвЊЭъГЩСљдТЗнЕФМІЕАЯњЪлШЮЮёЃЌФЧУДИУбјжГГЁдкЮхдТЗнвбгаЕФЯњЪлЕуЕФЛљДЁЩЯжСЩйдйдіМгЖрЩйИіЯњЪлЕуЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭМ1ЪЧвЛжжЭЦФЅЙЄОпФЃаЭЃЌЭМ2ЪЧЫќЕФЪОвтЭМЃЌвбжЊABЁЭPQЃЌAPЃНAQЃН3dmЃЌABЃН12dmЃЌЕуAдкжажсЯпlЩЯдЫЖЏЃЌЕуBдквдOЮЊдВаФЃЌOBГЄЮЊАыОЖЕФдВЩЯдЫЖЏЃЌЧвOBЃН4dmЃЎ
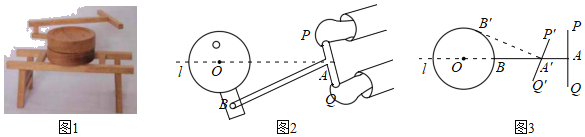
ЃЈ1ЃЉШчЭМ3ЃЌЕБЕуBАДФцЪБеыЗНЯђдЫЖЏЕНBЁфЪБЃЌAЁфBЁфгыЁбOЯрЧаЃЌдђAAЁфЃН__dmЃЎ
ЃЈ2ЃЉдкЕуBЕФдЫЖЏЙ§ГЬжаЃЌЕуPгыЕуOжЎМфЕФзюЖЬОрРыЮЊ__dmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпОЙ§![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§ЕуЃЎ
Ш§ЕуЃЎ
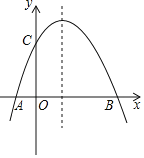
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯгавЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЕФжЕзюаЁЃЌЧѓЕу
ЕФжЕзюаЁЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉЕу![]() ЮЊ
ЮЊ![]() жсЩЯвЛЖЏЕуЃЌдкХзЮяЯпЩЯЪЧЗёДцдквЛЕу
жсЩЯвЛЖЏЕуЃЌдкХзЮяЯпЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙвд
ЃЌЪЙвд![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЫФЕуЙЙГЩЕФЫФБпаЮЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧѓЕу
ЫФЕуЙЙГЩЕФЫФБпаЮЮЊЦНааЫФБпаЮЃПШєДцдкЃЌЧѓЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com