
����Ŀ����ͼ��֪��������![]() �ύ�ڵ�C(0��4)����
�ύ�ڵ�C(0��4)����![]() �ύ��A(
�ύ��A(![]() ��0)��B(
��0)��B(![]() ��0)������
��0)������![]() ��
��![]() ����
����![]() ����������
����������
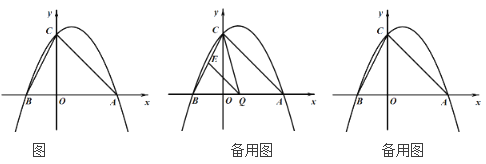
��1����������ߵĽ���ʽ��
��2����Q���߶�AB�ϵĶ��㣬����Q��QE��AC����BC�ڵ�E������CQ����Q(![]() ��0)����CQE�����Ϊ
��0)����CQE�����Ϊ![]() ����
����![]() ����
����![]() �ĺ�����ϵʽ����CQE����������ֵ��
�ĺ�����ϵʽ����CQE����������ֵ��
��3����M������Ϊ(2��0)���ʣ���ֱ��AC�ϣ��Ƿ���ڵ�F��ʹ�á�OMF�ǵ��������Σ������ڣ��������F�����꣬�������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() �� (����
�� (���У�![]() )����CQE����������ֵΪ3����3�����ڣ���F������Ϊ(1��3)��(2��2)��
)����CQE����������ֵΪ3����3�����ڣ���F������Ϊ(1��3)��(2��2)��
��������
��1���������÷������ͼ����x�ύ�����꣬������C������������a��ֵ���ɣ�
��2����EH��AB�ڵ�H���ɵ�EH��CO������QE��AC���ɵó�������ϵ���������EH�ij��ȣ����S��CQE���ó���ϵʽ���������ֵ��
��3�����ڣ����ô���ϵ�������AC�Ľ���ʽ����F��x��x��4������ʾ��OM��MF��OF�ij��ȣ�Ҫʹ��OMF�ǵ����������������������OF��FMʱ����OM��OF��2ʱ����OM��MFʱ���ֱ������F�����꣮
�⣺��1���ⷽ��![]() ��
��
�ã�![]() ��
��![]() ��
��
��A(4��0)��B(��2��0)��
�������߽���ʽΪ��![]() ��
��
��C(0��4)���룬��ã�![]() ��
��
�������߽���ʽΪ��
![]() ��
��![]() ��
��
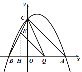
��2����Q(![]() ��0)���ɵã�
��0)���ɵã�
BQ��![]() ��AQ��
��AQ��![]() ��
��
��EH��AB�ڵ�H��
��EH��CO����![]() ��
��
�֡�QE��AC����![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]()
![]() ��
��
��![]() ����
����![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��
![]() ��
��
(����![]() )��
)��
���CQE����������ֵΪ3��
��3�����ڣ�
�������£�
��AC�Ľ���ʽΪ��![]() ��AC��A(4��0)��C(0��4)��
��AC��A(4��0)��C(0��4)��
��![]() ����֮�ã�
����֮�ã�![]() ��
��![]() ��
��
��AC�Ľ���ʽΪ��![]() ��
��
��![]() F��AC�ϣ���F(
F��AC�ϣ���F(![]() ��
��![]() )��
)��
��![]() ��
��
![]() ��
��![]() ��
��
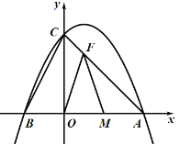
����OMF�ǵ��������ο��������������
��OF��FMʱ��F�ĺ�����ӦΪ1��
��F(1��3)��
��OF��OM��2ʱ��![]() ��
��
����ã�![]() ��
��
��![]() ����������������ڣ�
����������������ڣ�
�� OM��MF��2ʱ��![]() ��
��
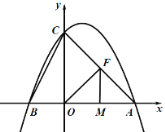
����ã�![]() ��
��
��ã�![]() ��
��![]() (��ȥ)��
(��ȥ)��
��F(2��2)��
��������������OMF�ǵ���������ʱ����F������Ϊ(1��3)��(2��2)��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ��ͼ�����ͬһ����ֱ��·�ϣ��״�ѧУȥͼ��ݣ��Ҵ�ͼ��ݻ�ѧУ���ס������˶����ٲ�����ͬʱ���������ȵ���Ŀ�ĵأ�����֮��ľ���y���ף���ʱ��t�����ӣ�֮��ĺ�����ϵ��ͼ��ʾ��
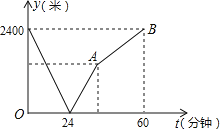
��1������ͼ����Ϣ����t���� ������ʱ�����������������ٶ�Ϊ�� ����/���ӣ��ҵ��ٶ�Ϊ�� ����/���ӣ�
��2��ͼ�е�A������Ϊ�� ����
��3�����߶�AB��ֱ�ߵĺ�������ʽ��
��4�������������У���ʱ�������400�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������ABCD�Ķ���ֱ�ΪA��0��1����B��-1��0����C��0��-1����D��1��0��������ͼ��M���������¶��壺PΪͼ��M������һ�㣬QΪ������ABCD��������һ�㣬���P��Q�����ľ��������ֵ����ô��������ֵΪͼ��M������������������d��M����
��1����֪��E��0��4����
��ֱ��д��d����E����ֵ��
��ֱ��y=kx+4��k��0����x�ύ�ڵ�F����d���߶�EF��ȡ��Сֵʱ����k��ȡֵ��Χ��
��2����T��Բ��ΪT(7��t)���뾶Ϊ1����d(��T)��11����ֱ��д��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊȫ��᳹���Ľ������룬�����������һ���Ľ�������ٽ�ѧ�������ɳ���������ʽ���ˮƽ���ɶ��е��������п�ʵʩ��������ֵ������60����1000�ף�Ů800�ף��ؿ�������������������ѡһ��������2019���^����ѧ�����꼶��ʼʵʩ��ij��ѧΪ�˽����꼶ѧ�������������˶���ϲ������������꼶ѧ���������ȡ����ѧ�����е����ʾ���ͨ������������������������ͳ��ͼ�����������ͳ��ͼ�е���Ϣ�ش��������⣺
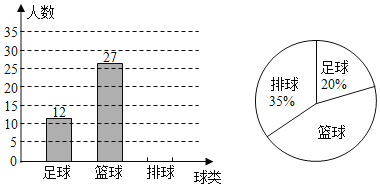
��1�����������ѧ���У�ϲ�������˶���ѧ������������ȫ����ͼ��
��2��������ѧ���꼶����400��ѧ����������Ƹ���ѧ���꼶ѧ����ϲ�������˶���ѧ���ж�������
��3������ϲ�������˶���2��������2��Ů���������ȡ2��ѧ����ȷ��Ϊ��У�����˶�Ա���ص��������������б�������״ͼ�ķ������ȡ������ѧ��Ϊһ��������һ��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����ѣ��˷�֧Ԯ�� �ں����人�¹ڷ������鱬���ڼ䣬���мס�������ҽԺ�ֱ���һ��һŮ��4��ҽ����Ա������֧Ԯ�����人�������������
��1�����Ӽס�����ҽԺ��Ԯ��ҽ����Ա�зֱ����ѡ1��������ѡ��2��ҽ����Ա�Ա���ͬ�ĸ����� ��
��2������Ԯ����4��ҽ����Ա�����ѡ2�������б�����״ͼ�ķ��������2��ҽ����Ա����ͬһ��ҽԺ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
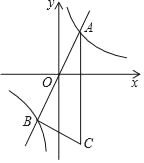
����Ŀ����ͼ��������������ͼ��������������y��2x��ͼ���ཻ��A��1��a����B���㣬��C�ڵ������ޣ�CA��y�ᣬ��ABC��90��
��1�����������Ľ���ʽ����B�����ꣻ
��2����tanC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
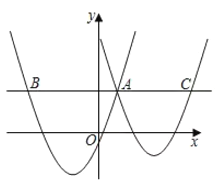
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() ���ڵ�A������A��
���ڵ�A������A��![]() ��Ĵ��ߣ��ֱ������������ڵ�B��C(��B�ڵ�A��࣬��C�ڵ�A�Ҳ�)�����߶�BC�ij�Ϊ____��
��Ĵ��ߣ��ֱ������������ڵ�B��C(��B�ڵ�A��࣬��C�ڵ�A�Ҳ�)�����߶�BC�ij�Ϊ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
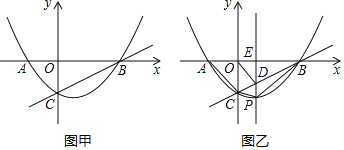
����Ŀ����ͼ�ף�������y��ax2+bx��1����A����1��0����B��2��0�����㣬��y���ڵ�C��
��1���������ߵı���ʽ��ֱ��BC�ı���ʽ��
��2����ͼ�ң���PΪ�ڵ����������������ϵ�һ�����㣬����P��x��Ĵ���PE��ֱ��BC�ڵ�D��
���ڵ�P�˶������У��ı���ACPB������Ƿ�������ֵ�������ڣ����������ֵ���������ڣ�˵�����ɣ�
���Ƿ���ڵ�Pʹ���Ե�O��C��DΪ������������ǵ��������Σ������ڣ�������������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
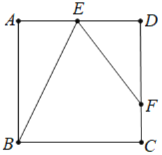
����Ŀ��������ABCD�У�EΪAD���е㣬��EΪ��������BEF=��EBC��EF��CD�ڵ�F��
��1����tan��BEF��
��2����DF��CF��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com