
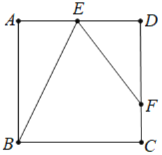
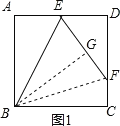
【题目】正方形ABCD中,E为AD的中点,以E为顶点作∠BEF=∠EBC,EF交CD于点F.
(1)求tan∠BEF;
(2)求DF:CF的值.
【答案】(1)2;(2)2.
【解析】
(1)先求得tan∠AEB=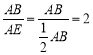 ,再证得∠BEF=∠AEB,即可求得答案;
,再证得∠BEF=∠AEB,即可求得答案;
(2)设AB=a,则AE=DE=![]() a,过点B作BG⊥EF于G,连接BF,推出△ABE≌△GBE,则AB=BG=a,AE=EG=
a,过点B作BG⊥EF于G,连接BF,推出△ABE≌△GBE,则AB=BG=a,AE=EG=![]() a,证出Rt△BGF≌Rt△BCF,得到GF=CF,根据勾股定理即可得到结果.
a,证出Rt△BGF≌Rt△BCF,得到GF=CF,根据勾股定理即可得到结果.
解:(1)∵在正方形ABCD中,
∴AD∥BC,∠A=90°,AB=AD,
∵E为AD的中点,
∴AE=![]() AD=
AD=![]() AB
AB
∴在Rt△ABE中,tan∠AEB=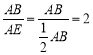
∵AD∥BC,
∴∠EBC=∠AEB,
∵∠BEF=∠EBC,
∴∠BEF=∠AEB,
∴tan∠BEF=tan∠AEB=2;
(2)如图1,设AB=a,则AE=DE=![]() a,
a,
过点B作BG⊥EF于G,连接BF,
∵∠FEB=∠EBC,AD∥BC,∠AEB=∠EBC,
∴∠AEB=∠BEF,
在△ABE与△GBE中
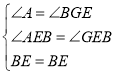 ,
,
∴△ABE≌△GBE,
∴AB=BG=a,AE=EG=![]() a,
a,
在Rt△BGF与Rt△BCF中
![]() ,
,
∴Rt△BGF≌Rt△BCF,
∴GF=CF,
设DF=b,则EF=![]() ,
,
∴GF=CF=EF﹣EG=![]() ﹣
﹣![]() a=a﹣b,
a=a﹣b,
∴a=![]() ,CF=a﹣b=
,CF=a﹣b=![]() b,
b,
∴DF:CF=b:![]() b=2.
b=2.


科目:初中数学 来源: 题型:
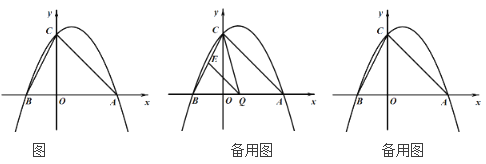
【题目】如图已知抛物线与![]() 轴交于点C(0,4),与
轴交于点C(0,4),与![]() 轴交于A(
轴交于A(![]() ,0)、B(
,0)、B(![]() ,0),其中
,0),其中![]() ,
,![]() 为方程
为方程![]() 的两个根.
的两个根.
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连结CQ,设Q(![]() ,0),△CQE的面积为
,0),△CQE的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式及△CQE的面积的最大值;
的函数关系式及△CQE的面积的最大值;
(3)点M的坐标为(2,0),问:在直线AC上,是否存在点F,使得△OMF是等腰三角形?若存在,请求出点F的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万kg与3.6万kg,现假定该养殖场蛋鸡产蛋量的月增长率相同.
(1)求该养殖场蛋鸡产蛋量的月平均增长率;
(2)假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万kg.如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一种推磨工具模型,图2是它的示意图,已知AB⊥PQ,AP=AQ=3dm,AB=12dm,点A在中轴线l上运动,点B在以O为圆心,OB长为半径的圆上运动,且OB=4dm.
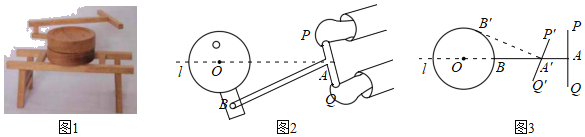
(1)如图3,当点B按逆时针方向运动到B′时,A′B′与⊙O相切,则AA′=__dm.
(2)在点B的运动过程中,点P与点O之间的最短距离为__dm.
查看答案和解析>>
科目:初中数学 来源: 题型:
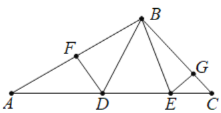
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,以点B为圆心,适当长为半径画弧交边于D,E两点(按照A,D,E,C依次排列,且D、E不重合).过D、E分别作AB和BC的垂线段交于F、G两点,如果线段DF=x,EG=y,则x、y的关系式为( )
A.20x-15y=![]() B.20x-15y=
B.20x-15y=![]()
C.15x-20y=![]() D.15x-20y=
D.15x-20y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
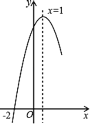
【题目】抛物线![]() 经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:
经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:
①![]() ;
;
②![]() >
>![]() ;
;
③若n>m>0,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值;
时的函数值;
④点(![]() ,0)一定在此抛物线上.
,0)一定在此抛物线上.
其中正确结论的个数是( )
A.4个B.3个
C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=![]() 的图像与
的图像与![]() 轴的一个交点为A(-1,0),另一个交点为B,与
轴的一个交点为A(-1,0),另一个交点为B,与![]() 轴交于点C(0,﹣3),顶点为D.
轴交于点C(0,﹣3),顶点为D.
(1)求二次函数的解析式和点D的坐标;
(2)若点M是抛物线在![]() 轴下方图像上的一动点,过点M作MN∥
轴下方图像上的一动点,过点M作MN∥![]() 轴交线段BC于点N,当MN取最大值时,点M 的坐标;
轴交线段BC于点N,当MN取最大值时,点M 的坐标;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点D落在x轴上,原抛物线上一点P平移后的对应点为Q,如果∠OQP=∠OPQ,试求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
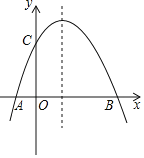
【题目】如图,抛物线经过![]() ,
,![]() ,
,![]() 三点.
三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点![]() ,使
,使![]() 的值最小,求点
的值最小,求点![]() 的坐标;
的坐标;
(3)点![]() 为
为![]() 轴上一动点,在抛物线上是否存在一点
轴上一动点,在抛物线上是否存在一点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 四点构成的四边形为平行四边形?若存在,求点
四点构成的四边形为平行四边形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
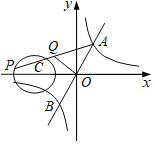
【题目】如图,一次函数y=2x与反比例函数y=![]() (k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为
(k>0)的图象交于A,B两点,点P在以C(﹣2,0)为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最大值为![]() ,则k的值为( )
,则k的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com