
【题目】如图:四边形ABCD中,E、F、G、H分别为各边的中点,顺次连接E、F、G、H,把四边形EFGH称为中点四边形.连接AC、BD,容易证明:中点四边形EFGH一定是平行四边形.
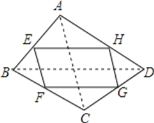
(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:当四边形ABCD的对角线满足AC=BD时,四边形EFGH为菱形.当四边形ABCD的对角线满足 时,四边形EFGH为矩形;当四边形ABCD的对角线满足 时,四边形EFGH为正方形;
(2)探索三角形AEH、三角形CFG与四边形ABCD的面积之间的等量关系,请写出你发现的结论,并加以证明;
(3)如果四边形ABCD的面积为2,那么中点四边形EFGH的面积是多少?
【答案】(1)AC⊥BD,AC⊥BD且 AC=BD;(2)S△AEH+S△CFG=![]() S四边形ABCD,见解析;(3)1
S四边形ABCD,见解析;(3)1
【解析】
(1)若四边形EFGH为矩形,则应有EF∥HG∥AC,EH∥FG∥BD,EF⊥EH,故应有AC⊥BD;若四边形EFGH为正方形,同上应有AC⊥BD,又应有EH=EF,而EF=![]() AC,EH=
AC,EH=![]() BD,故应有AC=BD.
BD,故应有AC=BD.
(2)由相似三角形的面积比等于相似比的平方求解.(3)由(2)可得SEFGH=![]() S四边形ABCD=1
S四边形ABCD=1
解:(1)若四边形EFGH为矩形,则应有EF∥HG∥AC,EH∥FG∥BD,EF⊥EH,故应有AC⊥BD;
若四边形EFGH为正方形,同上应有AC⊥BD,又应有EH=EF,而EF=![]() AC,EH=
AC,EH=![]() BD,故应有AC=BD.
BD,故应有AC=BD.
(2)S△AEH+S△CFG=![]() S四边形ABCD.
S四边形ABCD.
证明:在△ABD中,
∵EH=![]() BD,
BD,
∴△AEH∽△ABD.
∴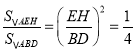 .
.
即S△AEH=![]() S△ABD
S△ABD
同理可证:S△CFG=![]() S△CBD
S△CBD
∴S△AEH+S△CFG=![]() (S△ABD+S△CBD)=
(S△ABD+S△CBD)=![]() S四边形ABCD.
S四边形ABCD.
(3)由(2)可知S△AEH+S△CFG=![]() (S△ABD+S△CBD)=
(S△ABD+S△CBD)=![]() S四边形ABCD,
S四边形ABCD,
同理可得S△BEF+S△DHG=(S△ABC+S△CDA)=
![]() S四边形ABCD,
S四边形ABCD,
故SEFGH=![]() S四边形ABCD=1.
S四边形ABCD=1.


科目:初中数学 来源: 题型:
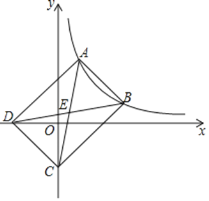
【题目】如图,点A和点B都是反比例函数![]() 在第一象限内图象上的点,点A的横坐标为1,点B的纵坐标为1,连接AB,以线段AB为边的矩形ABCD的顶点D,C恰好分别落在x轴,y轴的负半轴上,连接AC,BD交于点E,若
在第一象限内图象上的点,点A的横坐标为1,点B的纵坐标为1,连接AB,以线段AB为边的矩形ABCD的顶点D,C恰好分别落在x轴,y轴的负半轴上,连接AC,BD交于点E,若![]() 的面积为6,则k的值为( )
的面积为6,则k的值为( )
A.2B.3C.6D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
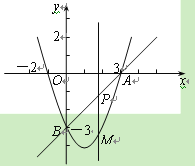
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、
B(0,-3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横
坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数图象经过(-2,4).
(1)如果点(a,1)和(-1,b)在函数图象上,求a,b的值;
(2)过图象上一点P作y轴的垂线,垂足为Q(0,-8),求△OPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,BG延长交CD于点F,CG延长交BD于点H,交AB于N.下列结论:①DE=CN;②![]() ;③S△DEC=3S△BNH;④∠BGN=45°;⑤
;③S△DEC=3S△BNH;④∠BGN=45°;⑤![]() .其中正确结论的个数有( )
.其中正确结论的个数有( )
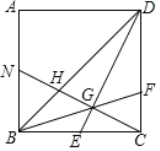
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点.∠APC=∠CPB=60°.
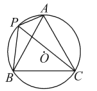
(1)判断△ABC的形状: ;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于![]() 的什么位置时,四边形APBC的面积最大?求出最大面积.
的什么位置时,四边形APBC的面积最大?求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,已知点F(2![]() ,0),直线GF交y轴正半轴于点G,且∠GFO=30°.
,0),直线GF交y轴正半轴于点G,且∠GFO=30°.
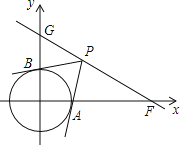
(1)直接写出点G的坐标;
(2)若⊙O的半径为1,点P是直线GF上的动点,直线PA、PB分别约⊙O相切于点A、B.
①求切线长PB的最小值;
②问:在直线GF上是够存在点P,使得∠APB=60°,若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com