【题目】如图，点A和点B都是反比例函数
在第一象限内图象上的点，点A的横坐标为1，点B的纵坐标为1，连接AB，以线段AB为边的矩形ABCD的顶点D，C恰好分别落在x轴，y轴的负半轴上，连接AC，BD交于点E，若
的面积为6，则k的值为（ ）
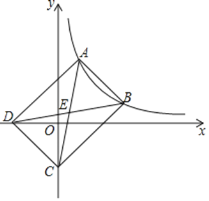
A.2B.3C.6D.12
【答案】B
【解析】
由点A的横坐标为1，点B的纵坐标为1，得出点E的坐标，进而推出点D的坐标，可以求出DA的长，，利用
列方程，可求出结果．
∵点A和点B都是反比例函数y＝
在第一象限内图象上的点，点A的横坐标为1，点B的纵坐标为1
∴A（1，k）、B（k，1）
E为矩形ABCD对角线的交点，
∴E（
，）
∵D，C恰好分别落在x轴，y轴的负半轴上，
设D（a，0），E为点A、C的中点
∴
，
∴a=1-k，
∴D（1-k，0），
∵A（1，k）、D（1-k，0），
∴AD2=（1-k-1）2+k2=
k2，
∴AD=
∵A（1，k）、B（k，1）
∴AB=
∴
∴k2-k-6=0
解得：k=3，k=-2（不符合题意，舍去）
故选B．
长江作业本同步练习册系列答案
小天才课时作业系列答案科目：初中数学 来源： 题型：
【题目】如图，抛物线
经过点
，与
轴相交于
，
两点，
（1）抛物线的函数表达式；
（2）点
在抛物线的对称轴上，且位于轴的上方，将
沿沿直线
翻折得到
，若点
恰好落在抛物线的对称轴上，求点
和点的坐标；
（3）设
是抛物线上位于对称轴右侧的一点，点
在抛物线的对称轴上，当
为等边三角形时，求直线
的函数表达式.
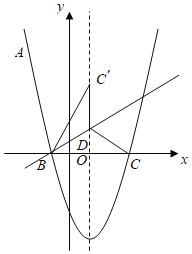
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，抛物线y= －
x2+bx+c与x轴负半轴交于A点，与x轴正半轴交于B点，与y轴正半轴交于C点，CO＝BO，AB=14．
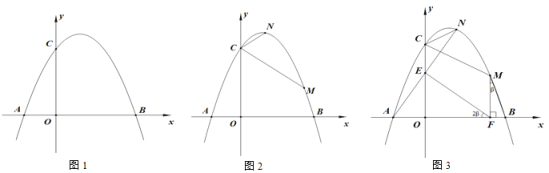
（1）求抛物线的解析式；
（2）如图2, 点M、N在第一象限内抛物线上，M在N点下方，连CM、CN，∠OCN+∠OCM＝180°， 设M点横坐标为m，N点横坐标为n，求m与n的函数关系式(n是自变量)；
（3）如图3, 在(2)条件下，连AN交CO于E，过M作MF⊥AB于F，连BM、EF，若∠AFE＝2∠FMB=2β， 求N点坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知Rt△AEC中，∠E＝90°，请按如下要求进行操作和判断：
（1）尺规作图：作△AEC的外接圆⊙O，并标出圆心O（不写画法）；
（2）延长CE，在CE的延长线上取点B，使EB＝EC，连结AB，设AB与⊙O的交点为D（标出字母B、D），判断：图中
与
相等吗？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
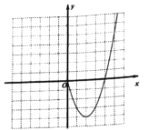
【题目】某课外学习小组根据学习函数的经验，对函数
的图象与性质进行了探究请补充完整以下探索过程：
（1）列表：
x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | m | 0 | -3 | -4 | -3 | 0 | -3 | -4 | n | 0 | … |
直接写出
________，
________；
（2）根据上表中的数据，在平面直角坐标系内补全该函数的图象，并结合图象写出该函数的两条性质：
性质1______________________________________________________
性质2_______________________________________________________
（3）若方程
有四个不同的实数根，请根据函数图象，直接写出k的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
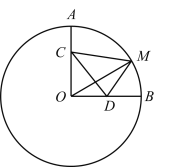
【题目】如图，在⊙O中，点A、点B在⊙O上，∠AOB＝90°，OA＝6，点C在OA上，且OC＝2AC，点D是OB的中点，点M是劣弧AB上的动点，则CM+2DM的最小值为_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场计划购进A、B两种新型节能台灯，已知B型节能台灯每盏进价比A型的多40元，且用3000元购进的A型节能台灯与用5000元购进的B型节能台灯的数量相同．
（1）求每盏A型节能台灯的进价是多少元？
（2）商场将购进A、B两型节能台灯100盏进行销售，A型节能台灯每盏的售价为90元，B型节能台灯每盏的售价为140元，且B型节能台灯的进货数量不超过A型节能台灯数量的2倍．应怎样进货才能使商场在销售完这批台灯时利最多？此时利润是多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
