
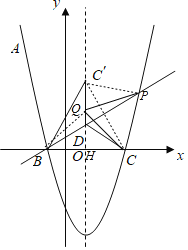
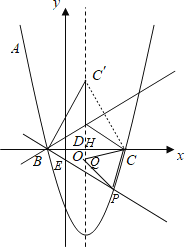
【题目】如图,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,
两点,
(1)抛物线的函数表达式;
(2)点![]() 在抛物线的对称轴上,且位于
在抛物线的对称轴上,且位于![]() 轴的上方,将
轴的上方,将![]() 沿沿直线
沿沿直线![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 恰好落在抛物线的对称轴上,求点
恰好落在抛物线的对称轴上,求点![]() 和点
和点![]() 的坐标;
的坐标;
(3)设![]() 是抛物线上位于对称轴右侧的一点,点
是抛物线上位于对称轴右侧的一点,点![]() 在抛物线的对称轴上,当
在抛物线的对称轴上,当![]() 为等边三角形时,求直线
为等边三角形时,求直线![]() 的函数表达式.
的函数表达式.
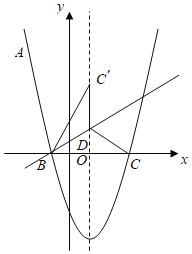
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为
的坐标为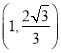 ;(3)直线
;(3)直线![]() 的函数表达式为
的函数表达式为![]() 或
或![]() .
.
【解析】
(1)根据待定系数法确定函数关系式即可求解;
(2)设抛物线的对称轴与![]() 轴交于点
轴交于点![]() ,则
,则![]() 点的坐标为
点的坐标为![]() ,
,![]() .
.
由翻折得![]() ,求出CH’的长,可得
,求出CH’的长,可得![]() ,求出DH的长,则可得D的坐标;
,求出DH的长,则可得D的坐标;
(3)由题意可知![]() 为等边三角形,分两种讨论①当点
为等边三角形,分两种讨论①当点![]() 在
在![]() 轴上方时,点
轴上方时,点![]() 在
在![]() 轴上方,连接
轴上方,连接![]() ,
,![]() ,证出
,证出![]() ,可得
,可得![]() 垂直平分
垂直平分![]() ,点
,点![]() 在直线
在直线![]() 上,可求出直线
上,可求出直线![]() 的函数表达式;②当点
的函数表达式;②当点![]() 在轴下方时,点
在轴下方时,点![]() 在
在![]() 轴下方,同理可求出另一条直线解析式.
轴下方,同理可求出另一条直线解析式.
(1)由题意,得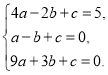
解得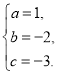
![]() 抛物线的函数表达式为
抛物线的函数表达式为![]() .
.
(2)![]() 抛物线与
抛物线与![]() 轴的交点为
轴的交点为![]() ,
,![]()
![]()
![]() ,抛物线的对称轴为直线
,抛物线的对称轴为直线![]() .
.
设抛物线的对称轴与![]() 轴交于点
轴交于点![]() ,则
,则![]() 点的坐标为
点的坐标为![]() ,
,![]() .
.
上翻折得![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() .’
.’
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
![]()
![]() .
.
由翻折得![]() .
.
在![]() 中,
中,![]() .
.
![]() 点
点![]() 的坐标为
的坐标为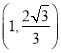 .
.
(3)取(2)中的点![]() ,
,![]() ,连接
,连接![]() .
.
![]()
![]() ,
,![]() .
.
![]()
![]() 为等边三角形,
为等边三角形,
分类讨论如下:
①当点![]() 在
在![]() 轴上方时,点
轴上方时,点![]() 在
在![]() 轴上方.
轴上方.
连接![]() ,
,![]()
![]()
![]() ,
,![]() 为等边三角形,
为等边三角形,
![]()
![]() ,
,![]() ,
,![]() .
.
![]()
![]() ,
,
![]()
![]() .
.
![]()
![]() ,
,
![]() 点
点![]() 在抛物线的对称轴上,
在抛物线的对称轴上,
![]()
![]() ,
,
![]()
![]() ,
,
又![]()
![]() ,
,
![]()
![]() 垂直平分
垂直平分![]() .
.
由翻折可知![]() 垂直平分
垂直平分![]() .
.
![]() 点
点![]() 在直线
在直线![]() 上,
上,
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
则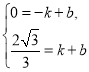 解得
解得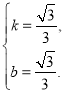
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() .
.
②当点![]() 在轴下方时,点
在轴下方时,点![]() 在
在![]() 轴下方.
轴下方.
![]()
![]() ,
,![]() 为等边三角形,
为等边三角形,
![]()
![]() ,
,![]() ,
,![]() .
.
![]()
![]() .
.
![]()
![]() .
.
![]()
![]() .
.
![]()
![]() ,
,![]()
![]()
![]() .
.
![]()
![]() .
.
设![]() 与
与![]() 轴相交于点
轴相交于点![]() .
.
在![]() 中,
中,![]()
![]() .
.
![]() 点
点![]() 的坐标为
的坐标为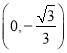 ,
,
设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
则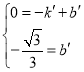 解得
解得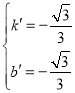
![]() 直线
直线![]() 的函数表达式为
的函数表达式为![]() .
.
综上所述,直线![]() 的函数表达式为
的函数表达式为![]() 或
或![]() .
.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】小颖“综合与实践”小组学习了三角函数后,开展了测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量.他们在该旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,如表是不完整测量数据.
课题 | 测量旗杆的高度 | |||
成员 | 组长:小颖,组员:小明,小刚,小英 | |||
测量工具 | 测量角度的仪器,皮尺等 | |||
测量示意图 |
| 说明: 线段GH表示学校旗杆,测量角度的仪器的高度AC=BD=1.62m,测点A,B与H在同一水平直线上,A,B之间的距离可以直接测得,且点G,H,A,B,C,D都在同一竖直平面内,点C,D,E在同一条直线上,点E在GH上. | ||
测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 |
∠GCE的度数 | 30.6° | 31.4° | 31° | |
∠GDE的度数 | 36.8° | 37.2° | 37° | |
A,B之间的距离 | 10.1m | 10.5m | m | |
… | … | |||
(1)任务一:完成表格中两次测点A,B之间的距离的平均值.
(2)任务二:根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆GH的高度.(精确到0.1m)(参考数据:sin31°≈0.51,cos31°≈0.86,tan31°≈0.60,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
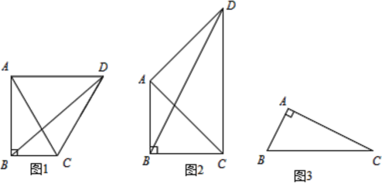
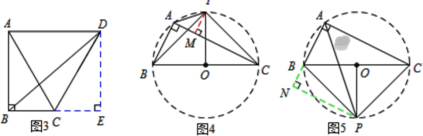
(1)如图1,在Rt△ABC中,∠BAC=30°,∠ABC=90°,将线段AC绕点A逆时针旋转,旋转角α=2∠BAC, ∠BCD的度数是 ;线段BD,AC之间的数量关系是 .
类比探究:
(2)在Rt△ABC中,∠BAC=45°,∠ABC=90°,将线段AC绕点A逆时针旋转,旋转角α=2∠BAC,请问(1)中的结论还成立吗?;
拓展延伸:
(3)如图3,在Rt△ABC中,AB=2,AC=4,∠BDC=90°,若点P满足PB=PC,∠BPC=90°,请直接写出线段AP的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学积极组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:

(1)求出x的值,并将不完整的条形统计图补充完整;
(2)若该校共有学生2500人,试估计每周课外阅读时间量满足2≤t<4的人数;
(3)若本次调查活动中,九年级(1)班的两个学习小组分别有3人和2人每周阅读时间量都在4小时以上,现从这5人中任选2人参加学校组织的知识抢答赛,求选出的2人来自不同小组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 于
于![]() ,交
,交![]() 轴于点
轴于点![]()
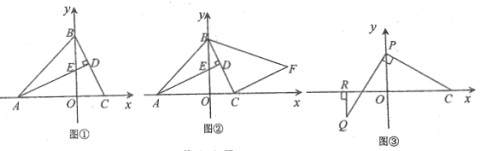
(1)如图①,求点![]() 的坐标;
的坐标;
(2)如图②:将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后得线段
后得线段![]() ,连接
,连接![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图③, 点![]() 为
为![]() 轴正半轴上一动点, 点
轴正半轴上一动点, 点![]() 在第二象限内,
在第二象限内,![]() 于
于![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
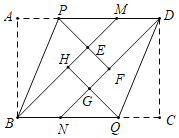
【题目】如图,在矩形纸片ABCD中,BM,DN分别平分∠ABC,∠CDA,沿BP折叠,点A恰好落在BM上的点E处,延长PE交DN于点F沿DQ折叠,点C恰好落在DN上的点G处,延长QG交BM于点H,若四边形EFGH恰好是正方形,且边长为1,则矩形ABCD的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
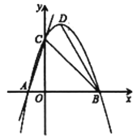
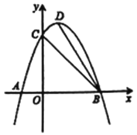
【题目】如图,一条抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 在
在![]() 轴上.
轴上.
(1)求抛物线解析式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() ,是否存在以点
,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(4)坐标平面内一点![]() 到点
到点![]() 的距离为1个单位,求
的距离为1个单位,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
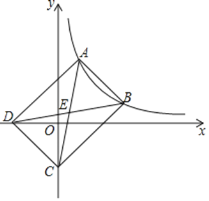
【题目】如图,点A和点B都是反比例函数![]() 在第一象限内图象上的点,点A的横坐标为1,点B的纵坐标为1,连接AB,以线段AB为边的矩形ABCD的顶点D,C恰好分别落在x轴,y轴的负半轴上,连接AC,BD交于点E,若
在第一象限内图象上的点,点A的横坐标为1,点B的纵坐标为1,连接AB,以线段AB为边的矩形ABCD的顶点D,C恰好分别落在x轴,y轴的负半轴上,连接AC,BD交于点E,若![]() 的面积为6,则k的值为( )
的面积为6,则k的值为( )
A.2B.3C.6D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com