
【题目】问题发现:
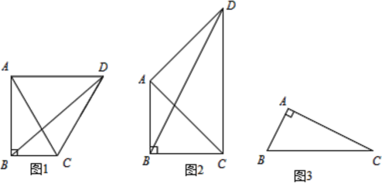
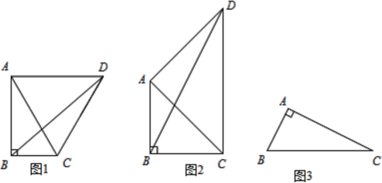
(1)如图1,在Rt△ABC中,∠BAC=30°,∠ABC=90°,将线段AC绕点A逆时针旋转,旋转角α=2∠BAC, ∠BCD的度数是 ;线段BD,AC之间的数量关系是 .
类比探究:
(2)在Rt△ABC中,∠BAC=45°,∠ABC=90°,将线段AC绕点A逆时针旋转,旋转角α=2∠BAC,请问(1)中的结论还成立吗?;
拓展延伸:
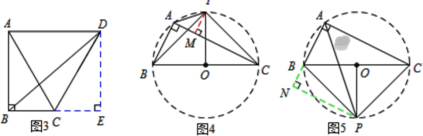
(3)如图3,在Rt△ABC中,AB=2,AC=4,∠BDC=90°,若点P满足PB=PC,∠BPC=90°,请直接写出线段AP的长度.
【答案】(1)120°,BD=![]() AC;(2)不成立,理由详见解析;(3)
AC;(2)不成立,理由详见解析;(3)![]() 或
或![]() .
.
【解析】
(1)过点D作DE⊥BC,通过线段之间的转换得到AC与DE之间的关系,在直角三角形BDE中通过BD与DE的关系,得到BD,AC之间的关系.
(2)类比(1)的解法,找线段之间的关系.
(3)分情况进行讨论,画出符合题意得图形进行求解.
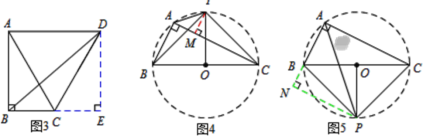
解:(1)如图3,过点D作DE⊥BC,垂足为E,设BC=m.
在Rt△ABC中,∠BAC=30°,由BC=AB·tan30°,BC=AC·sin30°,得AC=2m,BC=![]() m,
m,
∵AC=AD,∠CAD=2×30°=60°,∴△ACD为等边三角形,∴∠ACD=60°,CD=AC=2m,
∴∠BCD=60°×2=120°,在Rt△DEC中,∠DCE=180°-120°=60°,DC=2m,∴CE=CD·cos60°=m,DE=CE·tan60°=![]() m,∴在Rt△BED中,BD=
m,∴在Rt△BED中,BD=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,故BD=
,故BD=![]() AC.故答案为:120°;BD=
AC.故答案为:120°;BD=![]() AC.
AC.
(2)不成立,理由如下:
设BC=n,在Rt△ABC中,∠BAC=45°,∠ABC=90°,∴BC=AB=m,AC=![]() BC=
BC=![]() n,
n,
∵AC=AD,∠CAD=90°,∴△CAD为等腰直角三角形,∴∠ACD=45°,CD=![]() AC= 2n,
AC= 2n,
∴∠BCD=2×45°=90°,在Rt△BCD中,BD=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,,故BD=
,,故BD=![]() AC.答案为:90°;BD=
AC.答案为:90°;BD=![]() AC.故结论不成立.
AC.故结论不成立.
(3)AP的长为![]() 或
或![]() .;解答如下:
.;解答如下:
∵PB=PC,∴点P在线段BC的垂直平分线上,∵∠BAC=∠BCP=90°,故A、B、C、P四点共圆,以线段BC的中点为圆心构造⊙O,如图4,图5,分类讨论如下:
①当点P在直线BC上方时,如图4,作PM⊥AC,垂足为M,设PM=x.

∵PB=PC,∠BPC=90°,∴△PBC为等腰直角三角形,∴∠PBC=45°,
∵∠PAC=∠PBC=45°,∴△AMP为等腰直角三角形,∴AM=PM=x,AP=![]() PM=
PM=![]() x,
x,
在Rt△ABC中,AB=2,AC=4,∴BC=![]() =
=![]() ,∴PC=BC·sin45°=
,∴PC=BC·sin45°=![]() ,
,
在Rt△PMC中,∵∠PMC=90°,PM=x,PC=![]() ,CM=4-x,∴
,CM=4-x,∴![]() ,
,
解得:![]() ,
,![]() (舍),∴AP=
(舍),∴AP=![]() =
=![]() ;
;
②当点P在直线BC的下方时,如图5,作PN⊥AB的延长线,垂足为N,设PN=y.
同上可得PB=![]() ,△PAN为等腰三角形,∴AN=PN=y,∴BN=y-2,
,△PAN为等腰三角形,∴AN=PN=y,∴BN=y-2,
在Rt△PNB中,∵∠PNB=90°,PN=y,BN=y-2,PB=![]() ,∴
,∴![]() ,
,
解得:![]() ,
,![]() (舍),∴AP=
(舍),∴AP=![]() =
=![]() .故AP的长度为:
.故AP的长度为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】垦利区在进行“五城同创”的过程中,决定购买A,B两种树对某路段进行绿化改造,若购买A种树1棵,B种树3棵,需要2250元;购买A种树2棵,B种树5棵,需要3900元.
(1)求购买A,B两种树每棵各需多少元?
(2)考虑到绿化效果,购进A种树不能少于48棵,且用于购买这两种树的资金不低于52500元.若购进这两种树共100棵.问有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
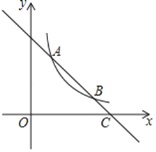
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 在第一象限的图象交于
在第一象限的图象交于![]() 和B两点,与
和B两点,与![]() 轴交于点C.
轴交于点C.
(1)求出反比例函数的解析式;
(2)若点P在![]() 轴上,且△APC的面积为5,求点P的坐标.
轴上,且△APC的面积为5,求点P的坐标.
(3)根据图象,直接写出使一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加西部博览会,资阳市计划印制一批宣传册.该宣传册每本共10页,由A、B两种彩页构成.已知A种彩页制版费300元/张,B种彩页制版费200元/张,共计2400元.(注:彩页制版费与印数无关)
(1)每本宣传册A、B两种彩页各有多少张?
(2)据了解,A种彩页印刷费2.5元/张,B种彩页印刷费1.5元/张,这批宣传册的制版费与印刷费的和不超过30900元.如果按到资阳展台处的参观者人手一册发放宣传册,预计最多能发给多少位参观者?
查看答案和解析>>
科目:初中数学 来源: 题型:
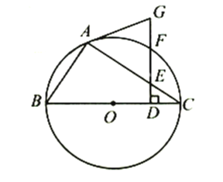
【题目】如图,![]() 为⊙
为⊙![]() 的内接三角形,
的内接三角形,![]() 为⊙
为⊙![]() 的直径,在线段
的直径,在线段![]() 上取点
上取点![]() (不与端点重合),作
(不与端点重合),作![]() ,分别交
,分别交![]() 、圆周于
、圆周于![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)已知![]() ,填空:
,填空:
①当![]() __________
__________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②若![]() ,当
,当![]() __________时,
__________时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() (k≠0)的图像与一次函数y=-x+b的图像在第一象限交于A、B两点,BC⊥x轴于点C,若△OBC的面积为2,且A点的纵坐标为4,B点的纵坐标为1.
(k≠0)的图像与一次函数y=-x+b的图像在第一象限交于A、B两点,BC⊥x轴于点C,若△OBC的面积为2,且A点的纵坐标为4,B点的纵坐标为1.
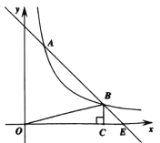
(1)求反比例函数、一次函数的表达式及直线AB与x轴交点E的坐标;
(2)已知点D(t,0)(t>0),过点D作垂直于x轴的直线,在第一象限内与一次函数y=-x+b的图像相交于点P,与反比函数![]() 上的图像相交于点Q,若点P位于点Q的上方,请结合函数图像直接写出此时t的取值范围.
上的图像相交于点Q,若点P位于点Q的上方,请结合函数图像直接写出此时t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
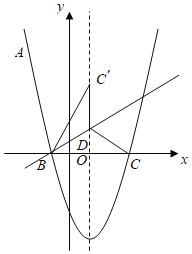
【题目】如图,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,
两点,
(1)抛物线的函数表达式;
(2)点![]() 在抛物线的对称轴上,且位于
在抛物线的对称轴上,且位于![]() 轴的上方,将
轴的上方,将![]() 沿沿直线
沿沿直线![]() 翻折得到
翻折得到![]() ,若点
,若点![]() 恰好落在抛物线的对称轴上,求点
恰好落在抛物线的对称轴上,求点![]() 和点
和点![]() 的坐标;
的坐标;
(3)设![]() 是抛物线上位于对称轴右侧的一点,点
是抛物线上位于对称轴右侧的一点,点![]() 在抛物线的对称轴上,当
在抛物线的对称轴上,当![]() 为等边三角形时,求直线
为等边三角形时,求直线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com