
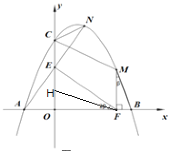
【题目】如图1,抛物线y= -![]() x2+bx+c与x轴负半轴交于A点,与x轴正半轴交于B点,与y轴正半轴交于C点,CO=BO,AB=14.
x2+bx+c与x轴负半轴交于A点,与x轴正半轴交于B点,与y轴正半轴交于C点,CO=BO,AB=14.
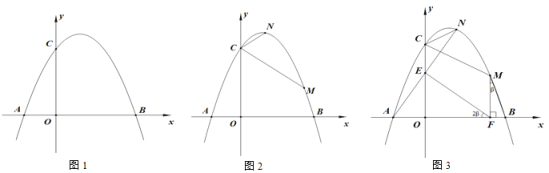
(1)求抛物线的解析式;
(2)如图2, 点M、N在第一象限内抛物线上,M在N点下方,连CM、CN,∠OCN+∠OCM=180°, 设M点横坐标为m,N点横坐标为n,求m与n的函数关系式(n是自变量);
(3)如图3, 在(2)条件下,连AN交CO于E,过M作MF⊥AB于F,连BM、EF,若∠AFE=2∠FMB=2β, 求N点坐标.
【答案】(1)![]() ;(2)m与n的函数关系式为
;(2)m与n的函数关系式为![]() ;(3)
;(3)![]() 的坐标为
的坐标为![]() .
.
【解析】
(1)根据题目给出条件用一个未知数舍出点A,B,C的坐标,代入解析式求解即可;
(2)根据题目给出特殊条件∠OCN+∠OCM=180°,得出直线![]() 与直线
与直线![]() 关于直线
关于直线![]() 对称,设点代入即可;
对称,设点代入即可;
(3)根据二倍角关系,在大角中构造相似三角形,大胆利用一个未知数求出线段长度,利用三角形的角平分线性质求解.
解:(1)设![]() ,则
,则![]() ;
;
将![]()
![]() 代入y= -
代入y= -![]() x2+bx+c得,
x2+bx+c得,
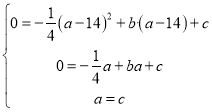 ;
;
解得: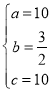 ;
;
∴抛物线的解析式:![]() ;
;
(2)∵∠OCN+∠OCM=180°;
可得直线![]() 与直线
与直线![]() 关于
关于![]() 对称;
对称;
设![]() ;
;
又![]() ;
;
可得![]() ;
;
设![]() ;
;
作点N关于![]() 的对称点
的对称点![]() ;
;
则![]() ;
;
又![]() 在
在![]() 上;
上;
![]() ;
;
化简得![]() ;
;
∴m与n的函数关系式为![]() ;
;
(3)![]() ;
;
![]() ;
;
在y正半轴上取一点H使得![]() ;
;
则有![]() ;
;
即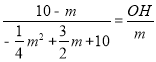 ;
;
解得![]() ;
;
设直线AN的解析式为:![]()
由![]() 可得
可得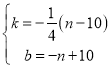 ;
;
![]() ;
;
又![]() ;
;
![]() ;
;
又![]() ;
;
![]() ;
;
在![]() 中,
中,![]() ;
;
由勾股定理可得![]() ;
;
![]() ;
;
![]() ;
;
又∵∠AFE=2∠FMB=2β;
![]() 平分
平分![]() ;
;
则有![]() ;
;
即![]() ;
;
解得![]() (舍),
(舍),![]() (舍),
(舍),![]() (舍),
(舍),![]() ;
;
![]() ;
;
![]() 的坐标为
的坐标为![]() .
.


科目:初中数学 来源: 题型:
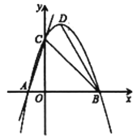
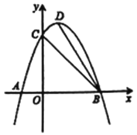
【题目】如图,一条抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 在
在![]() 轴上.
轴上.
(1)求抛物线解析式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() ,是否存在以点
,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(4)坐标平面内一点![]() 到点
到点![]() 的距离为1个单位,求
的距离为1个单位,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
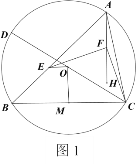
【题目】如图1,设![]() 是一个锐角三角形,且
是一个锐角三角形,且![]() ,
,![]() 为其外接圆,
为其外接圆,![]() 分别为其外心和垂心,
分别为其外心和垂心,![]() 为圆
为圆![]() 直径,
直径,![]() 为线段
为线段![]() 上一动点且满足
上一动点且满足![]() .
.
(1)证明:![]() 为
为![]() 中点;
中点;
(2)过![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,若
,若![]() 为
为![]() 的中点,证明:
的中点,证明: ![]() ;
;
(3)直线![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() (如图2),以
(如图2),以![]() 为直径的圆与圆
为直径的圆与圆![]() 的另一交点为
的另一交点为![]() .证明:若
.证明:若![]() 三线共点,则
三线共点,则![]() ;反之也成立.
;反之也成立.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小正方形边长均为1的方格纸中有线段AB,点A、B均在小正方形的顶点上.

(1)以AB为一边画Rt△ABC(点C在小正方形的顶点上),使△ABC的周长为![]() +5;
+5;
(2)在(1)的条件下,以AB为一边作△ABD,(点D在小正方形的顶点上),使![]() ,且△ABD的面积为2;连接CD,并直接写出∠ADC的正切值.
,且△ABD的面积为2;连接CD,并直接写出∠ADC的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“元旦大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有3张相同的卡片,卡片上分别标有“10元”、“20元”和“30元”的字样,规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里摸出一张卡片,记下钱数后放回,再从中摸出一张卡片.商场根据两张卡片所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客最多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于40元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A和点B都是反比例函数![]() 在第一象限内图象上的点,点A的横坐标为1,点B的纵坐标为1,连接AB,以线段AB为边的矩形ABCD的顶点D,C恰好分别落在x轴,y轴的负半轴上,连接AC,BD交于点E,若
在第一象限内图象上的点,点A的横坐标为1,点B的纵坐标为1,连接AB,以线段AB为边的矩形ABCD的顶点D,C恰好分别落在x轴,y轴的负半轴上,连接AC,BD交于点E,若![]() 的面积为6,则k的值为( )
的面积为6,则k的值为( )
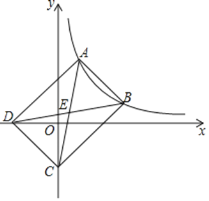
A.2B.3C.6D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是矩形
是矩形
(1)如图1,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
①求证:![]() ;
;
②若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() ;
;
(2)如图2,将矩形![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,点
处,点![]() 落在
落在![]() 边的点
边的点![]() 处,连接
处,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点.若
的中点.若![]() ,
,![]() ,直接写出
,直接写出![]() 的最小值为 .
的最小值为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com