
【题目】已知二次函数![]() 的图象如图所示,下列有
的图象如图所示,下列有![]() 个结论:①
个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .请你将正确结论的番号都写出来_______.
.请你将正确结论的番号都写出来_______.

【答案】①②③
【解析】
根据抛物线的性质逐一判断即可求解:①根据抛物线与x轴有两个交点可得![]() ,据此判断即可;②首先根据抛物线开口向上可得
,据此判断即可;②首先根据抛物线开口向上可得![]() ,然后根据抛物线对称轴为直线
,然后根据抛物线对称轴为直线![]() 可得
可得![]() ,最后由抛物线与y轴的交点在x轴上方可得
,最后由抛物线与y轴的交点在x轴上方可得![]() ,所以
,所以![]() ,据此即可判定;③根据二次函数
,据此即可判定;③根据二次函数![]() 可得当
可得当![]() 时,
时,![]() ,所以
,所以![]() ,据此判断即可;④首先根据当
,据此判断即可;④首先根据当![]() 时,
时,![]() ,可得
,可得![]() ,所以
,所以![]() ,然后根据无法确定
,然后根据无法确定![]() 是否等于﹣1,也就无法确定
是否等于﹣1,也就无法确定![]() 是否等于1,据此判断即可.
是否等于1,据此判断即可.
∵抛物线与x轴有两个交点
∴![]() ,
,
∴结论①正确;
∵抛物线开口向上
∴![]() ,
,
∵抛物线对称轴为直线![]()
∴![]() ,
,
∵抛物线与y轴的交点在x轴上方
∴![]() ,
,
∴![]() ,
,
∴结论②正确;
当![]() 时,
时,![]() ,
,
∴![]()
∴![]() ,
,
∴结论③正确;
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵无法确定![]() 是否等于﹣1,
是否等于﹣1,
∴也就无法确定![]() 是否等于1,
是否等于1,
∴结论④不正确.
故答案为:①②③


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1,抛物线y= -![]() x2+bx+c与x轴负半轴交于A点,与x轴正半轴交于B点,与y轴正半轴交于C点,CO=BO,AB=14.
x2+bx+c与x轴负半轴交于A点,与x轴正半轴交于B点,与y轴正半轴交于C点,CO=BO,AB=14.
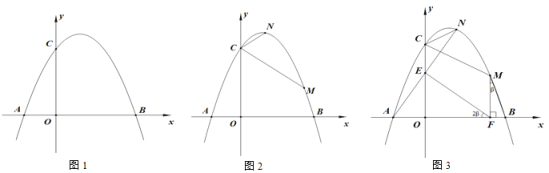
(1)求抛物线的解析式;
(2)如图2, 点M、N在第一象限内抛物线上,M在N点下方,连CM、CN,∠OCN+∠OCM=180°, 设M点横坐标为m,N点横坐标为n,求m与n的函数关系式(n是自变量);
(3)如图3, 在(2)条件下,连AN交CO于E,过M作MF⊥AB于F,连BM、EF,若∠AFE=2∠FMB=2β, 求N点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,点A、点B在⊙O上,∠AOB=90°,OA=6,点C在OA上,且OC=2AC,点D是OB的中点,点M是劣弧AB上的动点,则CM+2DM的最小值为_______.
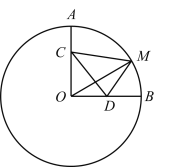
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.
(1)试求抛物线的解析式;
(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=![]() ,试求m的最大值及此时点P的坐标;
,试求m的最大值及此时点P的坐标;
(3)在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数![]() 的图象和
的图象和![]() 都在第一象限内,
都在第一象限内,![]() ,
,![]() 轴,且
轴,且![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
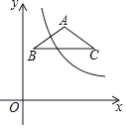
(1)若反比例函数![]() 的图象经过点B,求此反比例函数的解析式;
的图象经过点B,求此反比例函数的解析式;
(2)若将![]() 向下平移
向下平移![]() (m>0)个单位长度,
(m>0)个单位长度,![]() ,
,![]() 两点的对应点同时落在反比例函数图象上,求
两点的对应点同时落在反比例函数图象上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点O是对角线AC,BD的交点,点E在BC边上(点E不和BC的端点重合),且BE=![]() BC,连接AE交OB于点F,过点B作AE的垂线BG交OC于点G,连接GE.
BC,连接AE交OB于点F,过点B作AE的垂线BG交OC于点G,连接GE.
(1)求证:OF=OG;
(2)用含![]() 的代数式表示tan∠OBG的值;
的代数式表示tan∠OBG的值;
(3)如图2,当∠GEC=90°时,求![]() 的值.
的值.
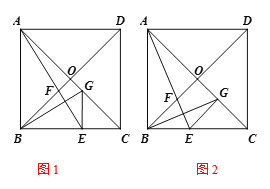
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A、B两种新型节能台灯,已知B型节能台灯每盏进价比A型的多40元,且用3000元购进的A型节能台灯与用5000元购进的B型节能台灯的数量相同.
(1)求每盏A型节能台灯的进价是多少元?
(2)商场将购进A、B两型节能台灯100盏进行销售,A型节能台灯每盏的售价为90元,B型节能台灯每盏的售价为140元,且B型节能台灯的进货数量不超过A型节能台灯数量的2倍.应怎样进货才能使商场在销售完这批台灯时利最多?此时利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
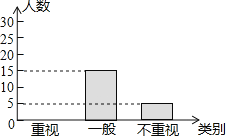
【题目】某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
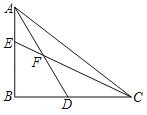
【题目】如图,在△ABC中,∠ABC=90°,D为BC的中点,点E在AB上,AD,CE交于点F,AE=EF=4,FC=9,则cos∠ACB的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com