
【题目】已知正比例函数图象经过(-2,4).
(1)如果点(a,1)和(-1,b)在函数图象上,求a,b的值;
(2)过图象上一点P作y轴的垂线,垂足为Q(0,-8),求△OPQ的面积.
【答案】(1)a=![]() ,b=2 ;(2) 16;
,b=2 ;(2) 16;
【解析】
(1)设正比比例函数的解析式为y=kx(k≠0),再把(-2,4)代入求出k的值,进而得出其解析式,把点(a,1)和(-1,b)代入求出a、b的值即可;
(2)把y=-8代入正比例函数的解析式求出x的值即可得出P点坐标,由三角形的面积公式即可得出结论.
(1)设正比比例函数的解析式为y=kx(k≠0),
∵正比例函数图象经过(-2,4),
∴4=-2k,
解得k=-2,
∴正比例函数的解析式为y=-2x.
∵点(a,1)和(-1,b)在函数图象上,
∴1=-2a,b=2,
解得a=![]() ,b=2;
,b=2;
(2)∵当y=-8时,x=4,
∴P(4,-8),
∴S△OPQ=![]() ×8×4=16.
×8×4=16.


科目:初中数学 来源: 题型:
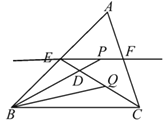
【题目】如图所示,在△ABC中,BC=4,E,F分别是AB,AC的中点,动点P在直线EF上,∠CBP的平分线交CE于点Q,当点Q把线段EC分成的两线段之比是1:2时,线段EP、BP满足的数量关系是__________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象与y轴相交于点(0,![]() 3),并经过点(
3),并经过点(![]() 2,5),它的对称轴是x=1,如图为函数图象的一部分.
2,5),它的对称轴是x=1,如图为函数图象的一部分.
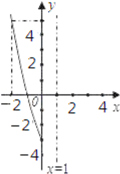
(1)求函数解析式,写出函数图象的顶点坐标;
(2)在图中,画出函数图象的其余部分;
(3)如果点P(n,![]() 2n)在上述抛物线上,求n的值.
2n)在上述抛物线上,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释效过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
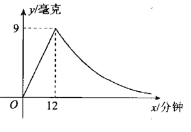
(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区有一块长方形水稻试验田,试验田的长、宽(如图所示,长度单位:米),试验田分两部分,一部分为水渠,另一部分为新型水稻种植田(阴影部分).
(1)用含a,b的式子表示新型水稻种植田的面积是多少平方米(结果化成最简形式);
(2)若a=30,b=40,在“农民丰收节”到来之时水稻成熟,计划先由甲型收割机收割一部分,再由乙型收割机收割剩余部分,甲型收割机收割水稻每平方米的费用为0.3元,乙型收割机收割水稻每平方米的费用为0.5元,若要收割全部水稻的费用不超过5000元,问甲型收割机最少收割多少平方米的水稻?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:四边形ABCD中,E、F、G、H分别为各边的中点,顺次连接E、F、G、H,把四边形EFGH称为中点四边形.连接AC、BD,容易证明:中点四边形EFGH一定是平行四边形.
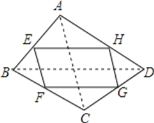
(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:当四边形ABCD的对角线满足AC=BD时,四边形EFGH为菱形.当四边形ABCD的对角线满足 时,四边形EFGH为矩形;当四边形ABCD的对角线满足 时,四边形EFGH为正方形;
(2)探索三角形AEH、三角形CFG与四边形ABCD的面积之间的等量关系,请写出你发现的结论,并加以证明;
(3)如果四边形ABCD的面积为2,那么中点四边形EFGH的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小亮两人用如图所示的两个分隔均匀的转盘做游戏:分别转动两个转盘,转盘停止后,将两个指针所指数字相加(若指针恰好停在分割线上,则重转一次).如果这两个数字之和小于8(不包括8),则小明获胜;否则小亮获胜。
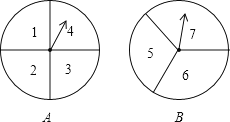
(1)利用列表法或画树状图的方法表示游戏所有可能出现的结果;
(2)这个游戏对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小区为了促进生活垃圾的分类处理,将生活垃圾分为厨余、可回收和其他三类,分别记为a,b,c,并且设置了相应的垃圾箱,“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若小明将一袋分好类的生活垃圾随机投入一类垃圾箱,请画树状图或列表求垃圾投放正确的概率;
(2)为调查居民生活垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总共100吨生活垃圾,数据统计如下表(单位:吨):
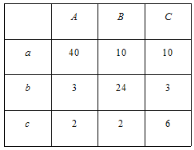
试估计该小区居民“厨余垃圾”投放正确的概率约是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
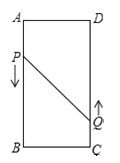
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(2)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com