
����Ŀ��С��Ϊ�˴ٽ����������ķ��ദ����������������Ϊ���ࡢ�ɻ��պ��������࣬�ֱ��Ϊa��b��c��������������Ӧ�������䣬�������������䡢���ɻ������͡������������䣬�ֱ��ΪA��B��C��
��1����С����һ���ֺ���������������Ͷ��һ�������䣬�뻭��״ͼ���б�������Ͷ����ȷ�ĸ��ʣ�
��2��Ϊ�������������������Ͷ��������������ȡ�˸�С���������������ܹ�100����������������ͳ�����±�����λ���֣���
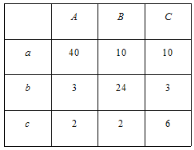
�Թ��Ƹ�С��������������Ͷ����ȷ�ĸ���Լ�Ƕ��٣�
���𰸡���1��P������Ͷ����ȷ����![]() ����2�����Ƹ�С��������������Ͷ����ȷ�ĸ���ԼΪ
����2�����Ƹ�С��������������Ͷ����ȷ�ĸ���ԼΪ![]() ��
��
��������
��1�����Ȼ�����״ͼ������״ͼ��֪����Ϊ9��Ͷ����ȷ����3�֣������������Ͷ����ȷ�Ĺ��ɣ�
��2�����������Լ����ʵĶ���������ɼ��ɡ�
��1����ͼ��ʾ��
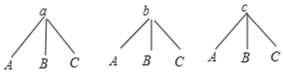
С����һ���ֺ���������������Ͷ��һ�������䣻����9�������
����Ͷ����ȷ����3�������
��P������Ͷ����ȷ����![]() ��
��![]() ��
��
��2����![]() ��
��
����Ƹ�С��������������Ͷ����ȷ�ĸ���ԼΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣬��y�ύ��C�㣬��A����1��0����
��x�ύ��A��B���㣬��y�ύ��C�㣬��A����1��0����
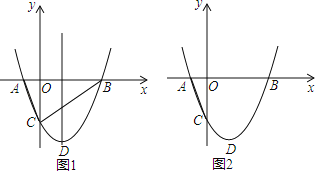
��1���������ߵĽ���ʽ������D�����ꣻ
��2���ж���ABC����״��֤����Ľ��ۣ�
��3����M�������߶Գ����ϵ�һ�����㣬��CM+AM��ֵ��Сʱ����M�����ꣻ
��4�����߶�BC�·�������������һ����P������PBC��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������ͼ����-2��4��.
(1)����㣨a��1���ͣ�-1��b���ں���ͼ���ϣ���a��b��ֵ��
(2)��ͼ����һ��P��y��Ĵ��ߣ�����ΪQ��0��-8�������OPQ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ʵ��ķ��������з��̣�
��1����x��3��2��24
��2��x2+12x+27��0
��3��x2+6x��4
��4��2��x��3��2��3��x��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���г�Ϊ24m����ʣ���һ������ǽ��ǽ�������ó���aΪ10m��Χ���м����һ����ʵij����λ��ԣ��軨�ԵĿ�ABΪxm�����ΪSm2��

��1��ҪΧ�����Ϊ45m2�Ļ��ԣ�AB�ij��Ƕ����ף�
��2����AB�ij��Ƕ���ʱ���Ե�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶Ϊ1��A��P��B��C�ǡ�O�ϵ��ĸ��㣮��APC=��CPB=60����
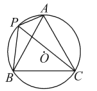
��1���ж���ABC����״�� ��
��2����̽���߶�PA��PB��PC֮���������ϵ����֤����Ľ��ۣ�
��3������Pλ��![]() ��ʲôλ��ʱ���ı���APBC�������������������
��ʲôλ��ʱ���ı���APBC�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BC�ǰ��O��ֱ������P�ǰ�Բ�����е㣬��A�ǻ�BP���е㣬AD��BC��D������AB��PB��AC��BP�ֱ���AD��AC�ཻ�ڵ�E��F��
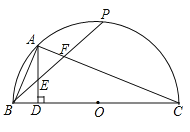
��1����֤��AE=BE��
��2���ж�BE��EF�Ƿ�����𣬲�˵�����ɣ�
��3��С��ͨ����������CF=2AB������С��ķ����Ƿ���ȷ������ȷ����˵�����ɣ�������ȷ����д��CF��AB��ȷ�Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
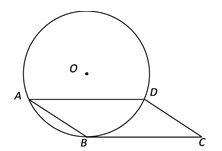
����Ŀ����ͼ������ABCD�У�AD�ǡ�O���ң�BC�ǡ�O�����ߣ��е�ΪB��
��1����֤��![]() ��
��
��2����AB��5��AD��8�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABCD��AB=6cm��AD=8cm����O�ӵ�B��������1cm/s���ٶ����C�˶�����O���˶�ʱ��Ϊt����λ��s����0<t<4�����Ե�OΪԲ�ģ�OBΪ�뾶����Բ��O��BC �ڵ�M������A����O�����߽�BC�ڵ�N���е�ΪP.

��1����ͼ2������N���C�غ�ʱ����t��
��2����ͼ3������AO����OQ![]() AO��AN�ڵ�Q������QM����֤��QM�ǡ�O�����ߣ�
AO��AN�ڵ�Q������QM����֤��QM�ǡ�O�����ߣ�
��3����ͼ4������CP���ڵ�O�����˶������У���CP����Сֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com