
【题目】用适当的方法解下列方程:
(1)(x﹣3)2=24
(2)x2+12x+27=0
(3)x2+6x=4
(4)2(x﹣3)2=3(x﹣3)
【答案】(1)x1=3+2![]() ,x2=3﹣2
,x2=3﹣2![]() (2)x1=﹣3,x2=﹣9 (3)x1=﹣3+
(2)x1=﹣3,x2=﹣9 (3)x1=﹣3+![]() ,x2=﹣3﹣
,x2=﹣3﹣![]() (4)x1=3,x2=4.5
(4)x1=3,x2=4.5
【解析】
(1)利用平方根的定义开方转化为两个一元一次方程,求出一次方程的解即可得到原方程的解;
(2)利用十字相乘法将方程左边的多项式分解因式,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解;
(3)方程左右两边都加上9,左边化为完全平方式,右边合并为一个非负常数,开方转化为两个一元一次方程,求出一次方程的解即可得到原方程的解;
(4)将方程右边的式子整体移项到左边,提取公因式化为积的形式,利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解;
解:(1)开方得:x﹣3=±2![]() ,
,
解得:x1=3+2![]() ,x2=3﹣2
,x2=3﹣2![]() ;
;
(2)分解因式得:(x+3)(x+9)=0,
解得:x1=﹣3,x2=﹣9;
(3)配方得:x2+6x+9=13,即(x+3)2=13,
开方得:x+3=±![]() ,
,
解得:x1=﹣3+![]() ,x2=﹣3﹣
,x2=﹣3﹣![]() ;
;
(4)方程整理得:2(x﹣3)2﹣3(x﹣3)=0,
分解因式得:(x﹣3)[2(x﹣3)﹣3]=0,
解得:x1=3,x2=4.5.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90,AC=BC=1,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点M,垂足分别为H、G.现有以下结论:①AB=![]() ;②当点E与点B重合时,MH=
;②当点E与点B重合时,MH=![]() ;③AF+BE=EF;④MGMH=
;③AF+BE=EF;④MGMH=![]() ,其中正确结论为( )
,其中正确结论为( )
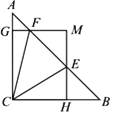
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
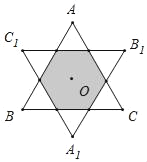
【题目】如图,O是边长为6的等边△ABC三边中垂线的交点,将△ABC绕点O逆时针方向旋转180°,得到△A1B1C1,则图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.

(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
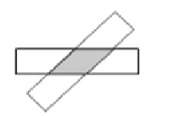
【题目】如图,将两张长为9,宽为3的矩形纸条交叉放置,其中重叠部分![]() 是一个菱形,则重叠部分菱形
是一个菱形,则重叠部分菱形![]() 周长最小值是__________,周长最大值是__________.
周长最小值是__________,周长最大值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知l1∥l2∥l3 , AB=3,BC=2,CD=1,那么下列式子中不成立的是( )

A.EC∶CG=5∶1;B.EF∶FG=1∶1;
C.EF∶FC=3∶2;D.EF∶EG=3∶5.
查看答案和解析>>
科目:初中数学 来源: 题型:
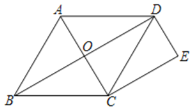
【题目】如图,菱形ABCD的对角线交于点O,点E是菱形外一点,DE∥AC,CE∥BD.
(1)求证:四边形DECO是矩形;
(2)连接AE交BD于点F,当∠ADB=30°,DE=3时,求菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.

(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB= ![]() FE.
FE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com