
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.

(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明.
【答案】(1)△ADE≌△BDE,△ABC∽△BCD;(2)证明见解析.
【解析】试题分析:(1)利用相似三角形的性质以及全等三角形的性质得出符合题意的答案;
(2)利用相似三角形的判定以及全等三角形的判定方法分别得出即可.
试题解析:解:(1)△ADE≌△BDE,△ABC∽△BCD;
(2)证明:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD为角平分线,
∴∠ABD=![]() ∠ABC=36°=∠A,
∠ABC=36°=∠A,
在△ADE和△BDE中
∵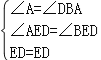 ,
,
∴△ADE≌△BDE(AAS);
证明:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD为角平分线,
∴∠DBC=![]() ∠ABC=36°=∠A,
∠ABC=36°=∠A,
∵∠C=∠C,
∴△ABC∽△BCD.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y=k1x+b的图象经过A(0,﹣2),B(1,0)两点,与反比例函数y=![]() 的图象在第一象限内的交点为M(m,4).
的图象在第一象限内的交点为M(m,4).
(1)求一次函数和反比例函数的表达式;
(2)在x轴上是否存在点P,使AM⊥MP?若存在,求出点P的坐标;若不存在,说明理由.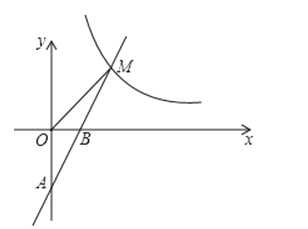
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)在数轴上,
(1)如果点A表示数2,动点B从点A出发向左移动5个单位长度,再向右移动8个单位长度,此时点B表示的数是 ,A、B两点间的距离是 ;
(2)一般的,如果点A表示数为a,动点B从点A出发向右移动b个单位长度,再向左移动c个单位长度,此时点B表示的数是 ,A.B两点间的距离是 (用a、b、c的式子表示).
(3)如果点A表示数-4 ,点B表示的数是8,那么A、B两点间的距离是 ,AB的中点所表示的数是 ;
(4)一般地,如果点A表示的数为a,点B表示的数是b,那么A、B两点间的距离是 ,AB的中点表示的数是 (用a、b的式子表示).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 按角分类,三角形可以分为钝角三角形、锐角三角形和等腰直角三角形
B. 按边分类,三角形可分为等腰三角形、不等边三角形和等边三角形
C. 三角形的外角大于任何一个内角
D. 一个三角形中至少有一个内角不大于60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了一次函数、二次函数、反比例函数后,爱钻研的小敏尝试用同样的方法研究函数y=![]() , 从而得出以下命题:
, 从而得出以下命题:
(1)当x>0时,y的值随着x的增大而减小;
(2)y的值有可能等于3;
(3)当x>0时,y的值随着x的增大越来越接近3;
(4)当y>0时,x>0或x<﹣![]() .
.
你认为真命题是( )
A.(1)(3)
B.(1)(4)
C.(1)(3)(4)
D.(2)(3)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:数x、y、z中较大的数称为max{x,y,z}.例如max{﹣3,1,﹣2}=1,函数y=max{﹣t+4,t,![]() }表示对于给定的t的值,代数式﹣t+4,t,
}表示对于给定的t的值,代数式﹣t+4,t,![]() 中值最大的数,如当t=1时y=3,当t=0.5时,y=6.则当t= 时函数y的值最小.
中值最大的数,如当t=1时y=3,当t=0.5时,y=6.则当t= 时函数y的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连接DE,作EF⊥DE,交直线AB于点F.
(1)若点F与B重合,求CE的长;(3分)
(2)若点F在线段AB上,且AF=CE,求CE的长.(5分)
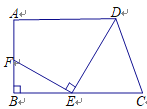
查看答案和解析>>
科目:初中数学 来源: 题型:
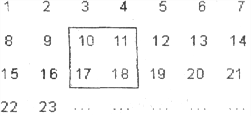
【题目】把正整数1,2,3,4,……,2009排列成如图所示的一个表
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是 , , 。
(2)当被框住的4个数之和等于416时,x的值是多少?
(3)被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两公司为“见义勇为基金会”各捐款60000元,已知乙公司比甲公司人均多捐40元,甲公司的人数比乙公司的人数多20%.
请你根据以上信息,提出一个用分式方程解决的问题,并写出解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com