
【题目】如图,已知l1∥l2∥l3 , AB=3,BC=2,CD=1,那么下列式子中不成立的是( )

A.EC∶CG=5∶1;B.EF∶FG=1∶1;
C.EF∶FC=3∶2;D.EF∶EG=3∶5.
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1(注:与图2完全相同),在直角坐标系中,抛物线经过点三点![]() ,
,![]() ,
,![]() .
.
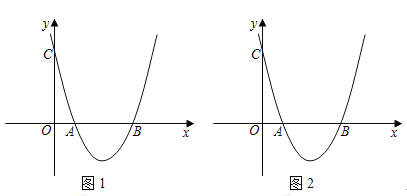
(1)求抛物线的解析式和对称轴;
(2)![]() 是抛物线对称轴上的一点,求满足
是抛物线对称轴上的一点,求满足![]() 的值为最小的点
的值为最小的点![]() 坐标(请在图1中探索);
坐标(请在图1中探索);
(3)在第四象限的抛物线上是否存在点![]() ,使四边形
,使四边形![]() 是以
是以![]() 为对角线且面积为
为对角线且面积为![]() 的平行四边形?若存在,请求出点
的平行四边形?若存在,请求出点![]() 坐标,若不存在请说明理由.(请在图2中探索)
坐标,若不存在请说明理由.(请在图2中探索)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
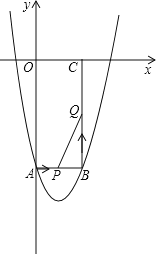
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=5,BC=6,D,E分别是边AB,AC上的两个动点(D不与A,B重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG.

(1)当FG与BC重合时,求正方形DEFG的边长;
(2)设AD=x,△ABC与正方形DEFG重叠部分的面积为y,试求y关于x的函数关系式,并写出x的取值范围;
(3)当△BDG是等腰三角形时,请直接写出AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.

(1)若∠A=60°,求BC的长;
(2)若sinA=![]() ,求AD的长.
,求AD的长.
(注意:本题中的计算过程和结果均保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC,∠C=90°,AC=BC=a,在△ABC中截出一个正方形A1B1C1D1,使点A1,D1分别在AC,BC边上,边B1C1在AB边上;在△BC1D1在截出第二个正方形A2B2C2D2,使点A2,D2分别在BC1,D1C1边上,边B2C2在BD1边上;…,依此方法作下去,则第n个正方形的边长为 .
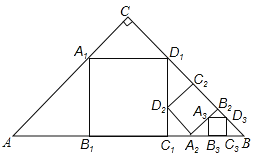
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com