
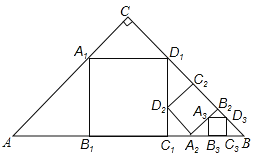
【题目】如图,△ABC,∠C=90°,AC=BC=a,在△ABC中截出一个正方形A1B1C1D1,使点A1,D1分别在AC,BC边上,边B1C1在AB边上;在△BC1D1在截出第二个正方形A2B2C2D2,使点A2,D2分别在BC1,D1C1边上,边B2C2在BD1边上;…,依此方法作下去,则第n个正方形的边长为 .
科目:初中数学 来源: 题型:
【题目】如图,已知l1∥l2∥l3 , AB=3,BC=2,CD=1,那么下列式子中不成立的是( )

A.EC∶CG=5∶1;B.EF∶FG=1∶1;
C.EF∶FC=3∶2;D.EF∶EG=3∶5.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
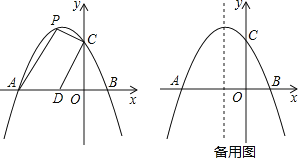
【题目】如图,抛物线y=ax2+bx+2交x轴于点A(-3,0)和点B(1,0),交y轴于点C.
(1)求这个抛物线的函数表达式.
(2)点D的坐标为(-1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值.
(3)点M为抛物线对称轴上的点,问:在抛物线上是否存在点N,使△MNO为等腰直角三角形,且∠MNO为直角?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰Rt△ABC,∠ACB=90°,CA=CB,以BC为边向外作等边△CBA,连接AD,过点C作∠ACB的角平分线与AD交于点E,连接BE.

(1)若AE=2,求CE的长度;
(2)以AB为边向下作△AFB,∠AFB=60°,连接FE,求证:FA+FB= ![]() FE.
FE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
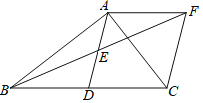
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的情况下,点M在AC线段上移动,请直接回答,当点M移动到什么位置时,MB+MD有最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣1.
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
(1)请在表内的空格中填入适当的数;
(2)根据列表,请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象;
(3)当x在什么范围内时,y随x增大而减小;
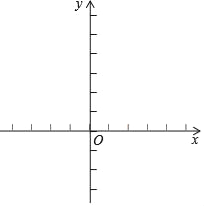
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,则下面说法正确的是( )
A. 1一定不是方程x2+bx+a=0的根B. 0一定不是方程x2+bx+a=0的根
C. ﹣1可能是方程x2+bx+a=0的根D. 1和﹣1都是方程x2+bx+a=0的根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com