
【题目】在平面直角坐标系中,O为坐标原点,已知点F(2![]() ,0),直线GF交y轴正半轴于点G,且∠GFO=30°.
,0),直线GF交y轴正半轴于点G,且∠GFO=30°.
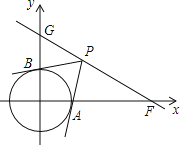
(1)直接写出点G的坐标;
(2)若⊙O的半径为1,点P是直线GF上的动点,直线PA、PB分别约⊙O相切于点A、B.
①求切线长PB的最小值;
②问:在直线GF上是够存在点P,使得∠APB=60°,若存在,请求出P点的坐标;若不存在,请说明理由.
【答案】(1)(0,2);(2)①PB的最小值为![]() ;②存在,P点坐标为(0,2)或(
;②存在,P点坐标为(0,2)或(![]() ,1).
,1).
【解析】
(1)根据含30度的直角三角形的三边的关系得到OG=![]() OF=2,于是得到G点坐标为(0,2);
OF=2,于是得到G点坐标为(0,2);
(2)连结OA、OB、OP,①由于PB为⊙O的切线,根据切线的性质得OB⊥PB,在Rt△POB中,根据勾股定理得PB=![]() ,则当OP最小时,PB最小,此时OP⊥FG,在Rt△OPF中,根据含30度的直角三角形的三边的关系得到OP=
,则当OP最小时,PB最小,此时OP⊥FG,在Rt△OPF中,根据含30度的直角三角形的三边的关系得到OP=![]() ,于是得到PB的最小值为
,于是得到PB的最小值为![]() ;②由于PA、PB为⊙O的切线,根据切线长定理得∠OPB=
;②由于PA、PB为⊙O的切线,根据切线长定理得∠OPB=![]() ∠APB=30°,在Rt△OPB中,根据含30度的直角三角形的三边的关系得OP=2OB=2,由于OG=2,所以点P在点G的位置时,满足要求,此时P点坐标为(0,2);由∠OFG=30°,可得∠OGF=60°,GF=2OG=4,加上OP=OG=2,于是可判断△OPG为等边三角形,则PG=OP=2,可判断点P为GF的中点,然后根据线段的中点坐标公式得到此时P点坐标为(
∠APB=30°,在Rt△OPB中,根据含30度的直角三角形的三边的关系得OP=2OB=2,由于OG=2,所以点P在点G的位置时,满足要求,此时P点坐标为(0,2);由∠OFG=30°,可得∠OGF=60°,GF=2OG=4,加上OP=OG=2,于是可判断△OPG为等边三角形,则PG=OP=2,可判断点P为GF的中点,然后根据线段的中点坐标公式得到此时P点坐标为(![]() ,1).
,1).
(1)∵点F的坐标为(2![]() ,0),
,0),
∴OF=2![]() ,
,
∵∠GFO=30°,
∴OG=![]() OF=2,
OF=2,
∴G点坐标为(0,2);
(2)连结OA、OB、OP,如图,
①∵PB为⊙O的切线,
∴OB⊥PB,
∴∠PBO=90°,
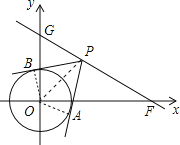
在Rt△POB中,OB=1,
∴PB=![]() ,
,
∴当OP最小时,PB最小,
此时OP⊥FG,
在Rt△OPF中,OF=2![]() ,∠OFP=30°,
,∠OFP=30°,
∴OP=![]() ,
,
∴PB的最小值为![]() ;
;
②存在.
∴PA、PB为⊙O的切线,
∴OP平分∠APB,
∴∠OPB=![]() ∠APB=
∠APB=![]() ×60°=30°,
×60°=30°,
在Rt△OPB中,OB=1,∠OPB=![]() ∠APB=30°,
∠APB=30°,
∴OP=2OB=2,
∵OG=2,
∴点P在点G的位置时,满足要求,此时P点坐标为(0,2);
∵∠OFG=30°,
∴∠OGF=60°,GF=2OG=4,
∵OP=OG=2,
∴△OPG为等边三角形,
∴PG=OP=2,
∴点P为GF的中点,
∴此时P点坐标为(![]() ,1),
,1),
综上所述,满足条件的P点坐标为(0,2)或(![]() ,1).
,1).


科目:初中数学 来源: 题型:
【题目】如图:四边形ABCD中,E、F、G、H分别为各边的中点,顺次连接E、F、G、H,把四边形EFGH称为中点四边形.连接AC、BD,容易证明:中点四边形EFGH一定是平行四边形.
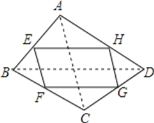
(1)如果改变原四边形ABCD的形状,那么中点四边形的形状也随之改变,通过探索可以发现:当四边形ABCD的对角线满足AC=BD时,四边形EFGH为菱形.当四边形ABCD的对角线满足 时,四边形EFGH为矩形;当四边形ABCD的对角线满足 时,四边形EFGH为正方形;
(2)探索三角形AEH、三角形CFG与四边形ABCD的面积之间的等量关系,请写出你发现的结论,并加以证明;
(3)如果四边形ABCD的面积为2,那么中点四边形EFGH的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2019年10月1日的建国70周年庆典上,有多国领导人出席观看了我国盛大的阅兵仪式.为表示友好,我国政府选择将刺绣和陶瓷两类工艺品作为国礼赠送给所有的来宾.甲,乙两个工厂分别承接了制作![]() ,
,![]() 两种刺绣与
两种刺绣与![]() 种陶瓷的任务.甲工厂安排100名工人制作刺绣,每人只能制作其中一种刺绣,乙工厂安排50名工人制作
种陶瓷的任务.甲工厂安排100名工人制作刺绣,每人只能制作其中一种刺绣,乙工厂安排50名工人制作![]() 种陶瓷.
种陶瓷.![]() 的人均制作数量比
的人均制作数量比![]() 的人均制作数量少3件,
的人均制作数量少3件,![]() 的人均制作量比
的人均制作量比![]() 的人均制作量少20%.若本次赠送的国礼(
的人均制作量少20%.若本次赠送的国礼(![]() ,
,![]() ,
,![]() 三样礼品)的人均制作数量比
三样礼品)的人均制作数量比![]() 的人均制作数量少30%,且
的人均制作数量少30%,且![]() 的人均制作数量为偶数件,则本次赠送的国礼共制作了_________件.
的人均制作数量为偶数件,则本次赠送的国礼共制作了_________件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(已有经验)
我们已经研究过作一个圆经过两个已知点,也研究过作一个圆与已知角的两条边都相切,尺规作图如图所示:
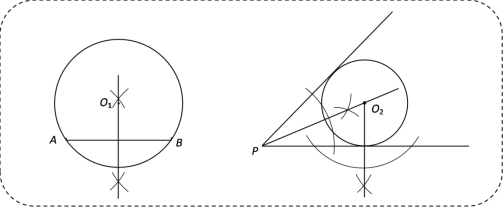
(迁移经验)
(1)如图①,已知点M和直线l,用两种不同的方法完成尺规作图:求作⊙O,使⊙O过M点,且与直线l相切.(每种方法作出一个圆即可,保留作图痕迹,不写作法)

(问题解决)
如图②,在Rt△ABC中,∠C=90°,AC=8,BC=6.
(2)已知⊙O经过点C,且与直线AB相切.若圆心O在△ABC的内部,则⊙O半径r的取值范围为 .
(3)点D是边AB上一点,BD=m,请直接写出边AC上使得∠BED为直角时点E的个数及相应的m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
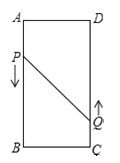
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(2)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB、BC是半径为![]() 的⊙O内的两条弦,且AB=6,BC=8.(1)若∠ABC=90°,则
的⊙O内的两条弦,且AB=6,BC=8.(1)若∠ABC=90°,则![]() =________;(2)若∠ABC=120°,则
=________;(2)若∠ABC=120°,则![]() =______.
=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4的正方形网格中,△ABC和△A'B'C'的顶点都在边长为1的小正方形的格点上.

(1)填空:∠BAC= °,AB= ;
(2)判断:△ABC和△A'B'C这两个三角形相似吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某购物商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元;为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件衬衫每降价1元,商场平均每天可多售出2件.
(1)每天销售这种衬衫的盈利要达到1200元,则每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场每天盈利最多?利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com