
ЁОЬтФПЁПФГЙКЮяЩЬГЁЯњЪлвЛХњУћХЦГФЩРЃЌЦНОљУПЬьПЩЪлГі20МўЃЌУПМўгЏРћ40дЊЃЛЮЊСЫРЉДѓЯњЪлЃЌдіМггЏРћЃЌОЁПьМѕЩйПтДцЃЌЩЬГЁОіЖЈВЩШЁЪЪЕБЕФНЕМлДыЪЉЃЎОЕїВщЗЂЯжЃЌУПМўГФЩРУПНЕМл1дЊЃЌЩЬГЁЦНОљУПЬьПЩЖрЪлГі2МўЃЎ
(1)УПЬьЯњЪлетжжГФЩРЕФгЏРћвЊДяЕН1200дЊЃЌдђУПМўГФЩРгІНЕМлЖрЩйдЊЃП
(2)УПМўГФЩРНЕМлЖрЩйдЊЪБЃЌЩЬГЁУПЬьгЏРћзюЖрЃПРћШѓЪЧЖрЩйЃП
ЁОД№АИЁПЃЈ1ЃЉ20.ЃЈ2ЃЉ15ЃЌ1250.
ЁОНтЮіЁП
ЃЈ1ЃЉЩшУПМўГФЩРгІНЕМлxдЊЃЌдђУПЬьЖрЯњЪл2xМўЃЌИљОнгЏРћ=УПМўЕФРћШѓЁСЪ§СПНЈСЂЗНГЬЧѓГіЦфНтМДПЩЃЛ
ЃЈ2ЃЉЩшУПМўГФЩРНЕМл![]() дЊЃЌЯњЪлРћШѓЮЊ
дЊЃЌЯњЪлРћШѓЮЊ![]() дЊЃЌИљОнЯњЪлРћШѓ=УПМўЕФРћШѓЁСЪ§СПБэЪОГіyгыxЕФЙиЯЕЪНЃЌгЩЖўДЮКЏЪ§ЕФаджЪМАКХЧѓГіНсТлЃЎ
дЊЃЌИљОнЯњЪлРћШѓ=УПМўЕФРћШѓЁСЪ§СПБэЪОГіyгыxЕФЙиЯЕЪНЃЌгЩЖўДЮКЏЪ§ЕФаджЪМАКХЧѓГіНсТлЃЎ
НтЃКЃЈ1ЃЉЩшУПМўГФЩРНЕМл![]() дЊЃЌ
дЊЃЌ
гЩЬтвтЃЌЕУ![]() .
.
НтЕУ![]() .
.
ЮЊСЫОЁСПМѕЩйПтДцЃЌЫљвдгІШЁ20.
Д№ЃКУПМўГФЩРгІНЕМл20дЊ.
ЃЈ2ЃЉЩшУПМўГФЩРНЕМл![]() дЊЃЌЯњЪлРћШѓЮЊ
дЊЃЌЯњЪлРћШѓЮЊ![]() дЊ.
дЊ.
дђ![]()
![]() .
.
Ёп![]() ,
,
ЁрyгазюДѓжЕЃЌЕБ![]() ЪБЃЌЦфзюДѓжЕЮЊ1250дЊ.
ЪБЃЌЦфзюДѓжЕЮЊ1250дЊ.
Д№ЃКУПМўГФЩРНЕМл15дЊЪБЃЌЯњЪлРћШѓЕФзюДѓжЕЮЊ1250дЊ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌвбжЊЕуFЃЈ2![]() ЃЌ0ЃЉЃЌжБЯпGFНЛyжсе§АыжсгкЕуGЃЌЧвЁЯGFO=30ЁуЃЎ
ЃЌ0ЃЉЃЌжБЯпGFНЛyжсе§АыжсгкЕуGЃЌЧвЁЯGFO=30ЁуЃЎ
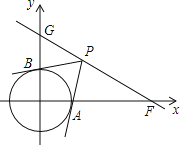
ЃЈ1ЃЉжБНгаДГіЕуGЕФзјБъЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ1ЃЌЕуPЪЧжБЯпGFЩЯЕФЖЏЕуЃЌжБЯпPAЁЂPBЗжБ№дМЁбOЯрЧагкЕуAЁЂBЃЎ
ЂйЧѓЧаЯпГЄPBЕФзюаЁжЕЃЛ
ЂкЮЪЃКдкжБЯпGFЩЯЪЧЙЛДцдкЕуPЃЌЪЙЕУЁЯAPB=60ЁуЃЌШєДцдкЃЌЧыЧѓГіPЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
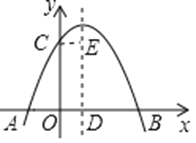
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+cЃЈaЁй0ЃЉгыyжсНЛгкЕуCЃЌгыxжсНЛгкAЃЌBСНЕуЃЌЦфжаЕуBЕФзјБъЮЊBЃЈ4ЃЌ0ЃЉЃЌХзЮяЯпЕФЖдГЦжсНЛxжсгкЕуDЃЌCEЁЮABЃЌВЂгыХзЮяЯпЕФЖдГЦжсНЛгкЕуEЃЎЯжгаЯТСаНсТлЃКЂйaЃО0ЃЛЂкbЃО0ЃЛЂл4a+2b+cЃМ0ЃЛЂмAD+CEЃН4ЃЎЦфжаЫљгае§ШЗНсТлЕФађКХЪЧЁЁ_____________________ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЯвCDЁЭABгкЕуEЃЌAMЪЧЁїACDЕФЭтНЧЁЯDAFЕФЦНЗжЯпЃЎ

ЃЈ1ЃЉЧѓжЄЃКAMЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєЁЯD = 60ЁуЃЌAD = 2ЃЌЩфЯпCOгыAMНЛгкNЕуЃЌЧыаДГіЧѓONГЄЕФЫМТЗЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
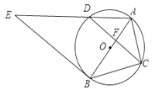
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌABОЙ§ЕуOЃЌCDЪЧЯвЃЌЧвCDЁЭABгкЕуFЃЌСЌНгADЃЌЙ§ЕуBЕФжБЯпгыЯпЖЮADЕФбгГЄЯпНЛгкЕуEЃЌЧвЁЯE=ЁЯACFЃЎ
ЃЈ1ЃЉШєCD=2![]() ЃЌ AF=3ЃЌЧѓЁбOЕФжмГЄЃЛ
ЃЌ AF=3ЃЌЧѓЁбOЕФжмГЄЃЛ
ЃЈ2ЃЉЧѓжЄЃКжБЯпBEЪЧЁбOЕФЧаЯпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНx2ЕФЭМЯѓШчЭМЫљЪОЃЎвбжЊAЕузјБъЮЊЃЈ1ЃЌ1ЃЉЃЌЙ§ЕуAзїAA1ЁЮxжсНЛХзЮяЯпгкЕуA1ЃЌЙ§ЕуA1зїA1A2ЁЮOAНЛХзЮяЯпгкЕуA2ЃЌЙ§ЕуA2зїA2A3ЁЮxжсНЛХзЮяЯпгкЕуA3ЃЌЙ§ЕуA3зїA3A4ЁЮOAНЛХзЮяЯпгкЕуA4ЁЁЃЌвРДЮНјааЯТШЅЃЌдђЕуA2019ЕФзјБъЮЊ_______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЛЛдЊЫМЯыЃЉдФЖСВФСЯЃК
ВФСЯ1 ШєвЛдЊЖўДЮЗНГЬ![]() ЕФСНИљЮЊ
ЕФСНИљЮЊ![]() ЁЂ
ЁЂ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() .
.
ВФСЯ2 вбжЊЪЕЪ§![]() ЁЂ
ЁЂ![]() Тњзу
Тњзу![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
НтЃКгЩЬтжЊ![]() ЁЂ
ЁЂ![]() ЪЧЗНГЬ
ЪЧЗНГЬ![]() ЕФСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌИљОнВФСЯ1ЃЌЕУ
ЕФСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌИљОнВФСЯ1ЃЌЕУ![]() ЃЌ
ЃЌ![]() .
.
Ёр![]() .
.
ИљОнЩЯЪіВФСЯНтОіЯТУцЕФЮЪЬтЃК
ЃЈ1ЃЉвЛдЊЖўДЮЗНГЬ![]() ЕФСНИљЮЊ
ЕФСНИљЮЊ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ![]() ___________ЃЛ
___________ЃЛ
ЃЈ2ЃЉвбжЊЪЕЪ§![]() ЃЌ
ЃЌ![]() Тњзу
Тњзу![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉвбжЊЪЕЪ§![]() ЃЌ
ЃЌ![]() Тњзу
Тњзу![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАбХзЮяЯпy=![]() x2ЦНвЦЕУЕНХзЮяЯпmЃЌХзЮяЯпmОЙ§ЕуAЃЈЉ6ЃЌ0ЃЉКЭдЕуOЃЈ0ЃЌ0ЃЉЃЌЫќЕФЖЅЕуЮЊPЃЌЫќЕФЖдГЦжсгыХзЮяЯпy=
x2ЦНвЦЕУЕНХзЮяЯпmЃЌХзЮяЯпmОЙ§ЕуAЃЈЉ6ЃЌ0ЃЉКЭдЕуOЃЈ0ЃЌ0ЃЉЃЌЫќЕФЖЅЕуЮЊPЃЌЫќЕФЖдГЦжсгыХзЮяЯпy=![]() x2НЛгкЕуQЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЁЁ Ёј ЁЁЃЎ
x2НЛгкЕуQЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЁЁ Ёј ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП5GЪБДњМДНЋРДСйЃЌКўББЪЁЬсГіЁАНЈГЩШЋЙњСьЯШЁЂжаВПвЛСї5GЭјТчЁБЕФеНТдФПБъЃЎОнЭГМЦЃЌФПЧАКўББ5GЛљеОЕФЪ§СПга1.5ЭђзљЃЌМЦЛЎЕН2020ФъЕзЃЌШЋЪЁ5GЛљеОЪ§ЪЧФПЧАЕФ4БЖЃЌЕН2022ФъЕзЃЌШЋЪЁ5GЛљеОЪ§СПНЋДяЕН17.34ЭђзљЃЎ
(1)АДееМЦЛЎЃЌЧѓ2020ФъЕзЕН2022ФъЕзЃЌШЋЪЁ5GЛљеОЪ§СПЕФФъЦНОљдіГЄТЪЃЛ
(2)Шє2023ФъБЃГжЧАСНФъ5GЛљеОЪ§СПЕФФъЦНОљдіГЄТЪВЛБфЃЌЕН2023ФъЕзЃЌШЋЪЁ5GЛљеОЪ§СПФмЗёГЌЙ§29ЭђзљЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com