
【题目】5G时代即将来临,湖北省提出“建成全国领先、中部一流5G网络”的战略目标.据统计,目前湖北5G基站的数量有1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座.
(1)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率;
(2)若2023年保持前两年5G基站数量的年平均增长率不变,到2023年底,全省5G基站数量能否超过29万座?
【答案】(1)2020年底到2022年底,全省5G基站数量的年平均增长率为70%(2)到2023年底,全省5G基站数量能超过29万座.
【解析】
(1)根据增长率问题:变化前的量×(1+x)2=变化后的量,列出方程求解.
(2)按照(1)中算出的增长率,计算2023年的基站数,即可判断.
(1)设2020年底到2022年底,全省5G基站数量的年平均增长率为x,
依题意,得:1.5×4×(1+x)2=17.34
解得:x1=0.7=70%,x2=-2.7(舍去).
答:2020年底到2022年底,全省5G基站数量的年平均增长率为70%.
(2)![]() (万座)
(万座)
29.478万座>29万座
答:到2023年底,全省5G基站数量能超过29万座.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
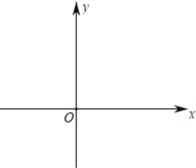
【题目】在平面直角坐标系xOy中(如图),已知抛物线y=﹣![]() +bx+c(其中b、c是常数)经过点A(﹣2,﹣2)与点B(0,4),顶点为M.
+bx+c(其中b、c是常数)经过点A(﹣2,﹣2)与点B(0,4),顶点为M.
(1)求该抛物线的表达式与点M的坐标;
(2)平移这条抛物线,得到的新抛物线与y轴交于点C(点C在点B的下方),且△BCM的面积为3.新抛物线的对称轴l经过点A,直线l与x轴交于点D.
①求点A随抛物线平移后的对应点坐标;
②点E、G在新抛物线上,且关于直线l对称,如果正方形DEFG的顶点F在第二象限内,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.

(1)根据图象信息,当t= 分钟时甲乙两人相遇,甲的速度为 米/分钟,乙的速度为 米/分钟;
(2)图中点A的坐标为 ;
(3)求线段AB所直线的函数表达式;
(4)在整个过程中,何时两人相距400米?
查看答案和解析>>
科目:初中数学 来源: 题型:
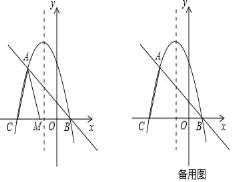
【题目】在平面直角坐标系中,我们定义直线y=ax﹣a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2
x+2![]() 与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,点A的坐标为 ,点B的坐标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
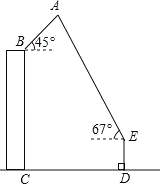
【题目】4月18日,一年一度的“风筝节”活动在市政广场举行,如图,广场上有一风筝A,小江抓着风筝线的一端站在D处,他从牵引端E测得风筝A的仰角为67°,同一时刻小芸在附近一座距地面30米高(BC=30米)的居民楼顶B处测得风筝A的仰角是45°,已知小江与居民楼的距离CD=40米,牵引端距地面高度DE=1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.414).
≈1.414).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
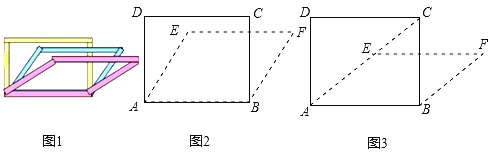
【题目】如图1,由于四边形具有不稳定性,因此在同一平面推矩形的边可以改变它的形状(推移过程中边的长度保持不变).已知矩形ABCD,AB=4cm,AD=3cm,固定边AB,推边AD,使得点D落在点E处,点C落在点F处.
(1)如图2,如果∠DAE=30°,求点E到边AB的距离;
(2)如图3,如果点A、E、C三点在同一直线上,求四边形ABFE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com