
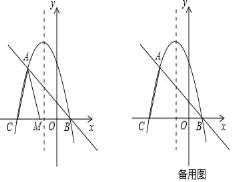
【题目】在平面直角坐标系中,我们定义直线y=ax﹣a为抛物线y=ax2+bx+c(a、b、c为常数,a≠0)的“梦想直线”;有一个顶点在抛物线上,另有一个顶点在y轴上的三角形为其“梦想三角形”.已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2
x+2![]() 与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
与其“梦想直线”交于A、B两点(点A在点B的左侧),与x轴负半轴交于点C.
(1)填空:该抛物线的“梦想直线”的解析式为 ,点A的坐标为 ,点B的坐标为 ;
(2)如图,点M为线段CB上一动点,将△ACM以AM所在直线为对称轴翻折,点C的对称点为N,若△AMN为该抛物线的“梦想三角形”,求点N的坐标;
(3)当点E在抛物线的对称轴上运动时,在该抛物线的“梦想直线”上,是否存在点F,使得以点A、C、E、F为顶点的四边形为平行四边形?若存在,请直接写出点E、F的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(﹣2,
;(﹣2,![]() );(1,0);(2)N点坐标为(0,
);(1,0);(2)N点坐标为(0,![]() ﹣3)或(
﹣3)或(![]() ,
,![]() );(3)存在;E(﹣1,﹣
);(3)存在;E(﹣1,﹣![]() )、F(0,
)、F(0,![]() )或E(﹣1,﹣
)或E(﹣1,﹣![]() )、F(﹣4,
)、F(﹣4,![]() ).
).
【解析】
(1)由梦想直线的定义可求得其解析式,联立梦想直线与抛物线解析式可求得A、B的坐标;
(2)当N点在y轴上时,过A作AD⊥y轴于点D,则可知AN=AC,结合A点坐标,则可求得ON的长,可求得N点坐标;当M点在y轴上即,M点在原点时,过N作NP⊥x轴于点P,由条件可求得∠NMP=60°,在Rt△NMP中,可求得MP和NP的长,则可求得N点坐标;
(3)当AC为平行四边形的一边时,过F作对称轴的垂线FH,过A作AK⊥x轴于点K,可证△EFH≌△ACK,可求得DF的长,则可求得F点的横坐标,从而可求得F点坐标,由HE的长可求得E点坐标;当AC为平行四边形的对角线时,设E(﹣1,t),由A、C的坐标可表示出AC中点,从而可表示出F点的坐标,代入直线AB的解析式可求得t的值,可求得E、F的坐标.
解:(1)∵抛物线![]() ,
,
∴其梦想直线的解析式为![]() ,
,
联立梦想直线与抛物线解析式可得: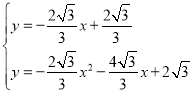 ,
,
解得: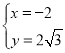 或
或![]() ,
,
∴A(﹣2,![]() ),B(1,0),
),B(1,0),
故答案为:![]() ;(﹣2,
;(﹣2,![]() );(1,0);
);(1,0);
(2)当点N在y轴上时,△AMN为梦想三角形,
如图1,过A作AD⊥y轴于点D,则AD=2,
在![]() 中,
中,
令y=0可求得x=﹣3或x=1,
∴C(﹣3,0),且A(﹣2,![]() ),
),
∴AC=![]() =
=![]() ,
,
由翻折的性质可知AN=AC=![]() ,
,
在Rt△AND中,由勾股定理可得DN=![]() =
=![]() =3,
=3,
∵OD=![]() ,
,
∴ON=![]() ﹣3或ON=
﹣3或ON=![]() +3,
+3,
当ON=![]() +3时,则MN>OD>CM,与MN=CM矛盾,不合题意,
+3时,则MN>OD>CM,与MN=CM矛盾,不合题意,
∴N点坐标为(0,![]() ﹣3);
﹣3);
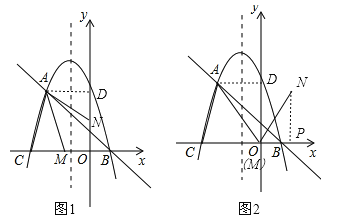
当M点在y轴上时,则M与O重合,过N作NP⊥x轴于点P,如图2,
在Rt△AMD中,AD=2,OD=![]()
∴∠DAM=60°,
∵AD∥x轴,
∴∠AMC=∠DAO=60°,
又由折叠可知∠NMA=∠AMC=60°,
∴∠NMP=60°,且MN=CM=3,
∴MP=![]() MN=
MN=![]() ,NP=
,NP=![]() MN=
MN=![]() ,
,
∴此时N点坐标为(![]() ,
,![]() );
);
综上可知N点坐标为(0,![]() ﹣3)或(
﹣3)或(![]() ,
,![]() );
);
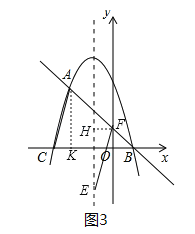
(3)①当AC为平行四边形的边时,如图3,过F作对称轴的垂线FH,过A作AK⊥x轴于点K,
则有AC∥EF且AC=EF,
∴∠ACK=∠EFH,
在△ACK和△EFH中,
∵∠ACK=∠EFH,∠AKC=∠EHF,AC=EF,
∴△ACK≌△EFH(AAS),
∴FH=CK=1,HE=AK=![]() ,
,
∵抛物线对称轴为x=﹣1,
∴F点的横坐标为0或﹣2,
∵点F在直线AB上,
∴当F点横坐标为0时,则F(0,![]() ),此时点E在直线AB下方,
),此时点E在直线AB下方,
∴E到y轴的距离为EH﹣OF=![]() ﹣
﹣![]() =
=![]() ,
,
即E点纵坐标为﹣![]() ,
,
∴E(﹣1,﹣![]() );
);
当F点的横坐标为﹣2时,则F与A重合,不合题意,舍去;
②当AC为平行四边形的对角线时,
∵C(﹣3,0),且A(﹣2,![]() ),
),
∴线段AC的中点坐标为(﹣2.5,![]() ),
),
设E(﹣1,t),F(x,y),
则x﹣1=2×(﹣2.5),y+t=![]() ,
,
∴x=﹣4,y=![]() ﹣t,
﹣t,
代入直线AB解析式可得![]() ﹣t=﹣
﹣t=﹣![]() ×(﹣4)+
×(﹣4)+![]() ,
,
解得t=﹣![]() ,
,
∴E(﹣1,﹣![]() ),F(﹣4,
),F(﹣4,![]() );
);
综上可知存在满足条件的点F,此时E(﹣1,﹣![]() )、F(0,
)、F(0,![]() )或E(﹣1,﹣
)或E(﹣1,﹣![]() )、F(﹣4,
)、F(﹣4,![]() ).
).


科目:初中数学 来源: 题型:
【题目】甲、乙两位同学进校时需要从学校大门A、B、C三个入口处中的任意一处测量体温,体温正常方可进校.
(1)甲同学在A入口处测量体温的概率是 ;
(2)求甲、乙两位同学在同一入口处测量体温的概率.(用“画树状图”或“列表”的方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中点![]() ,
,![]() ,以
,以![]() 为顶点在第一象限内作正方形
为顶点在第一象限内作正方形![]() .反比例函数
.反比例函数![]() 、
、![]() 分别经过
分别经过![]() 、
、![]() 两点(1)如图2,过
两点(1)如图2,过![]() 、
、![]() 两点分别作
两点分别作![]() 、
、![]() 轴的平行线得矩形
轴的平行线得矩形![]() ,现将点
,现将点![]() 沿
沿![]() 的图象向右运动,矩形
的图象向右运动,矩形![]() 随之平移;
随之平移;
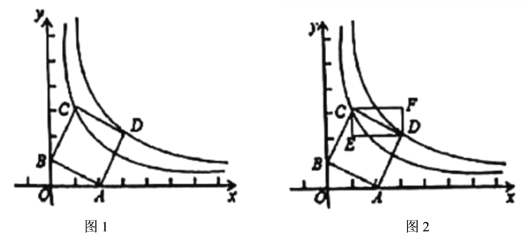
①试求当点![]() 落在
落在![]() 的图象上时点
的图象上时点![]() 的坐标_____________.
的坐标_____________.
②设平移后点![]() 的横坐标为
的横坐标为![]() ,矩形的边
,矩形的边![]() 与
与![]() ,
,![]() 的图象均无公共点,请直接写出
的图象均无公共点,请直接写出![]() 的取值范围____________.
的取值范围____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实践小组想利用镜子的反射测量池塘边一棵树的高度AB.测量和计算的部分步骤如下:

①如图,树与地面垂直,在地面上的点C处放置一块镜子,小明站在BC的延长线上,当小明在镜子中刚好看到树的顶点A时,测得小明到镜子的距离CD=2米,小明的眼睛E到地面的距离ED=1.5米;
②将镜子从点C沿BC的延长线向后移动10米到点F处,小明向后移动到点H处时,小明的眼睛G又刚好在镜子中看到树的顶点A,这时测得小明到镜子的距离FH=3米;
③计算树的高度AB;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5G时代即将来临,湖北省提出“建成全国领先、中部一流5G网络”的战略目标.据统计,目前湖北5G基站的数量有1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座.
(1)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率;
(2)若2023年保持前两年5G基站数量的年平均增长率不变,到2023年底,全省5G基站数量能否超过29万座?
查看答案和解析>>
科目:初中数学 来源: 题型:
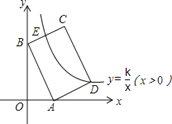
【题目】如图,在平面直角坐标系中,矩形ABCD的边AB:BC=3:2,点A(3,0),B(0,6)分别在x轴,y轴上,反比例函数y=![]() (x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
(x>0)的图象经过点D,且与边BC交于点E,则点E的坐标为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
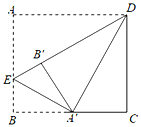
【题目】如图,在矩形ABCD中,AD=2.将∠A向内翻折,点A落在BC上,记为A′,折痕为DE.若将∠B沿EA′向内翻折,点B恰好落在DE上,记为B′,则AB=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
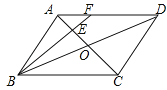
A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
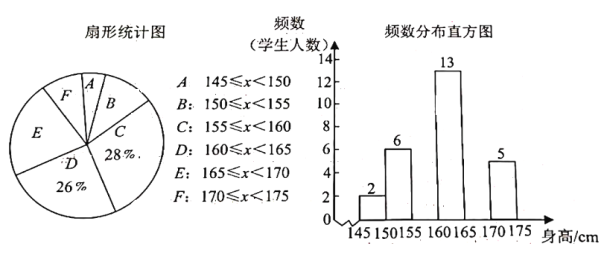
【题目】体育老师统计了七年级甲、乙两个班女生的身高情况,并绘制了如下不完整的统计图.请根据图中信息,解决下列问题:
(1)求甲、乙两个班共有女生多少人?
(2)请将频数分布直方图补充完整;
(3)求扇形统计图中![]() 部分所对应的扇形圆心角的度数.
部分所对应的扇形圆心角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com