
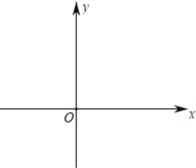
����Ŀ����ƽ��ֱ������ϵxOy��(��ͼ)����֪������y����![]() +bx+c(����b��c�dz���)������A(��2����2)���B(0��4)������ΪM��
+bx+c(����b��c�dz���)������A(��2����2)���B(0��4)������ΪM��
��1����������ߵı���ʽ���M�����ꣻ
��2��ƽ�����������ߣ��õ�������������y�ύ�ڵ�C(��C�ڵ�B���·�)������BCM�����Ϊ3���������ߵĶԳ���l������A��ֱ��l��x�ύ�ڵ�D��
�����A��������ƽ�ƺ�Ķ�Ӧ�����ꣻ
����E��G�����������ϣ��ҹ���ֱ��l�Գƣ����������DEFG�Ķ���F�ڵڶ������ڣ����F�����꣮
���𰸡���1��![]() ������M�������ǣ�(2��6)����2������A��Ӧ�������Ϊ(��6����5)����F(��2��
������M�������ǣ�(2��6)����2������A��Ӧ�������Ϊ(��6����5)����F(��2��![]() )��
)��
��������
��1������������y����![]() +bx+c(����b��c�dz���)������A(��2����2)���B(0��4)���Ӷ�������������ߵĽ���ʽ��Ȼ����ʽ��Ϊ����ʽ�����ɵõ�����M�����ꣻ
+bx+c(����b��c�dz���)������A(��2����2)���B(0��4)���Ӷ�������������ߵĽ���ʽ��Ȼ����ʽ��Ϊ����ʽ�����ɵõ�����M�����ꣻ
��2���������������ߵĶԳ���l������A���ɵ��������ߵĶ���Ϊ(-2,k)����ƽ�ƺ��������ߵĽ���ʽΪ![]() ���ɵ�C�����꣬������з������k���Ӷ����Եõ���A��������ƽ�ƺ�Ķ�Ӧ�����ꣻ
���ɵ�C�����꣬������з������k���Ӷ����Եõ���A��������ƽ�ƺ�Ķ�Ӧ�����ꣻ
����������������ε����ʣ���F(��2��2a)��E(��2+a��a)����E���루2���Ľ���ʽ�м������a���̶����⣮������õ�F�����꣮
�⣺��1����A(��2����2)��B(0��4)����![]() �У�
�У�
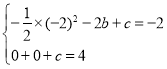
���![]()
���������ߵı���ʽΪ��![]() ��
��
��y��![]() x2+2x+4��
x2+2x+4��![]() (x��2)2+6��
(x��2)2+6��
������M�������ǣ�(2��6)��
��2���١�ƽ�ƺ������ߵĶԳ��ᾭ����A(��2����2)��
������ƽ�ƺ�������߱���ʽΪ��![]() ��
��
��C(0����2+k)��
��![]() ��
��
��ã�k��3��
��![]() ��
��
��ԭ����������ƽ��4����λ������ƽ��3����λ���Եõ��µ������ߣ�
����A��Ӧ�������Ϊ(��6����5)��
����EG��DF�Ľ���ΪH�� ��������DEFG�У�EG��DF��EG��DF��2EH��2DH��
����E��G�������������ϵ�һ�ԶԳƵ㣬
��EG��x�ᣮ
��DF��x�ᣬ
��F(��2��2a)��
����F�ڵڶ������ڣ�
��a��0��
��EG��DF��2EH��2DH��2a��
�������E�ڵ�G���Ҳ࣬��ôE(��2+a��a)��
����E����![]() ����
����![]() ��
��
��ã�![]() ��
��![]() (�������⣬��ȥ)��
(�������⣬��ȥ)��
��F(��2��![]() )��
)��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǡ�O���ڽ������Σ�AB�ǡ�O��ֱ����OF��AB����AC�ڵ�F����E��AB���ӳ����ϣ�����EM������C���ҡ�ACE+��AFO��180����
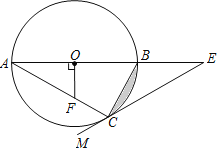
��1����֤��EM�ǡ�O�����ߣ�
��2������A����E����O�İ뾶Ϊ1������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ű�����ȫ��ͬ��ֽ��![]() ��������ֱ����ĸ���ͬ�ļ���ͼ�Σ���������ֽ�Ʊ��泯��ϴ��.
��������ֱ����ĸ���ͬ�ļ���ͼ�Σ���������ֽ�Ʊ��泯��ϴ��.
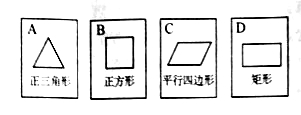
��1�������������һ�ţ�������������ͼ�������ĶԳ�ͼ�εĸ��ʣ�
��2��С����С��Լ����һ����Ϸ�������Ϊ������С���������һ��ֽ�ƣ����Żأ�����С����ʣ�µ�ֽ�����������һ�ţ�����������������ͼ�ζ�����Գ�ͼ��С����ʤ������С����ʤ�������Ϸ��ƽ�������б���������״ͼ��˵�����ɣ�ֽ����![]() ��ʾ��.
��ʾ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���������Ա���xȡaʱ������ֵyҲ����a�����dz�aΪ��������IJ�����.������κ���y��x2+2x+c����������IJ�����x1��x2����x1��1��x2����c��ȡֵ��Χ��( )
A. c����3B. c����2C. c��![]() D. c��1
D. c��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�Ƶ�A��ʱ����ת�õ���ADE�����е�B��C�ֱ����D��E��Ӧ�����B��D��C����ǡ����ͬһֱ���ϣ���ô���н��۴�����ǣ� ��
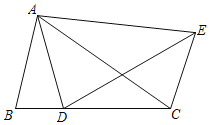
A.��ACB����AEDB.��BAD����CAE
C.��ADE����ACED.��DAC����CDE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�����λͬѧ��Уʱ��Ҫ��ѧУ����A��B��C������ڴ��е�����һ���������£������������ɽ�У��
��1����ͬѧ��A��ڴ��������µĸ����� ��
��2����ס�����λͬѧ��ͬһ��ڴ��������µĸ��ʣ�����������״ͼ�������б����ķ���д���������̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�У���BAC=90�����ó߹����A��һ��ֱ�ߣ�ʹ�佫��ABC�ֳ��������Ƶ������Σ�����������ȷ����_______��������ţ�
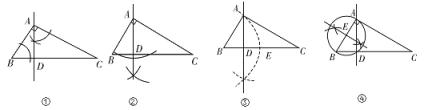
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ѵ�С��ͬ����30�Ƚǵ����ǰ���ͼ���ã���ͼ����AO��2����N���߶�OD�ϣ���NO��1����P���߶�AB�ϵ�һ�����㣬����COD�̶�����AOB�Ƶ�O��ʱ����ת�Ĺ����У��߶�PN���ȵ����ֵ��_____����Сֵ��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��5Gʱ���������٣�����ʡ���������ȫ�����ȡ��в�һ��5G���硱��ս��Ŀ�꣮��ͳ�ƣ�Ŀǰ����5G��վ��������1.5�������ƻ���2020��ף�ȫʡ5G��վ����Ŀǰ��4������2022��ף�ȫʡ5G��վ�������ﵽ17.34������
(1)���ռƻ�����2020���2022��ף�ȫʡ5G��վ��������ƽ�������ʣ�
(2)��2023�걣��ǰ����5G��վ��������ƽ�������ʲ��䣬��2023��ף�ȫʡ5G��վ�����ܷ�29������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com