
【题目】某中学库存一批旧桌凳,准备修理后捐助贫困山区学校.现有甲、乙两个木工小组都想承揽这项业务,经协商得知:甲小组单独修理这批桌凳比乙小组多用20天,乙小组每天比甲小组多修8套,甲小组每天修16套桌凳;学校每天需付甲小组修理费80元,付乙小组120元.
(1)求甲、乙两个木工小组单独修理这批桌凳各需多少天.
(2)在修理桌凳的过程中,学校要委派一名维修工进行质量监督,并由学校负担他每天10元的生活补助.现有下面三种修理方案供选择:
①由甲小组单独修理;②由乙小组单独修理;③由甲、乙两小组合作修理.
你认为哪种方案既省时又省钱?试比较说明.
【答案】(1)60天,40天;(2)方案③既省时又省钱.
【解析】
(1)设甲小组单独修完需要x天,乙小组单独修完需要y天,根据“甲小组单独修理这批桌凳比乙小组多用20天”,以及桌凳总数不变,便可建立方程组进行解答;
(2)综合(1)所得求出这批旧桌凳的数目,然后求出三种方案的工作时间与实际花费,再进行比较即可.
解:(1)设甲小组单独修理这批桌凳需要x天,乙小组单独修理这批桌凳需要y天.
根据题意,得![]()
解得![]()
答:甲、乙两个木工小组单独修理这批桌凳各需60天、40天.
(2)这批旧桌凳的数目为60×16=960(套).
方案①:学校需付费用为60×(80+10)=5400(元);
方案②:学校需付费用为40×(120+10)=5200(元);
方案③:学校需付费用为![]() ×(120+80+10)=5040(元).
×(120+80+10)=5040(元).
比较知,方案③既省时又省钱.
故答案为:(1)60天,40天;(2)方案③既省时又省钱.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】将-1、![]() 、
、![]() 、2、
、2、![]() 、
、![]() ……按下面的规律排列,若规定(m,n)表示第m排从左至右的第n个数,那么表示(7,2)和(8,4)的数的积是____________.
……按下面的规律排列,若规定(m,n)表示第m排从左至右的第n个数,那么表示(7,2)和(8,4)的数的积是____________.
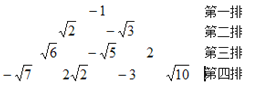
查看答案和解析>>
科目:初中数学 来源: 题型:
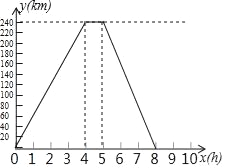
【题目】一辆货车从A地运货到240km的B地,卸货后返回A地,如图中实线是货车离A地的路程y(km)关于出发后的时间x(h)之间的函数图象.货车出发时,正有一个自行车骑行团在AB之间,距A地40km处,以每小时20km的速度奔向B地.
(1)货车去B地的速度是 ,卸货用了 小时,返回的速度是 ;
(2)求出自行车骑行团距A地的路程y(km)关于x的函数关系式,并在此坐标系中画出它的图象;
(3)求自行车骑行团与货车迎面相遇,是货车出发后几小时后,自行车骑行团还有多远到达B地.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点E(3,2)在双曲线y=![]() (x>0)上。过动点P(t,0)作x轴的垂线分别与该双曲线和直线y=
(x>0)上。过动点P(t,0)作x轴的垂线分别与该双曲线和直线y=![]() x交于A.、B两点,以线段AB为对角线作正方形ADBC,当正方形ADBC的边(不包括正方形顶点)经过点E时,则t的值为___.
x交于A.、B两点,以线段AB为对角线作正方形ADBC,当正方形ADBC的边(不包括正方形顶点)经过点E时,则t的值为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,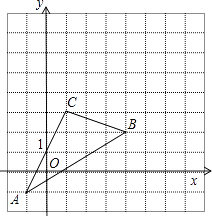
(1)请写出△ABC各点的坐标;
(2)求出S△ABC;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道1+2+3+…+![]() =
=![]() ,则1+2+3+…+10= ___________ .
,则1+2+3+…+10= ___________ .
[问题提出] 那么 ![]() 的结果等于多少呢?
的结果等于多少呢?
[阅读理解] 在图1所示的三角形数阵中,第1行圆圈中的数为1,即12 ;第2行两个圆圈中数的和为2+2,即22;......;第n行n个圆圈中数的和为n+n+![]() n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ .
n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ .
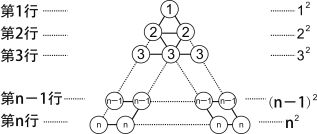
图1
[规律探究] 将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n-1行的第一个圆圈中的数分别为n-1,2,n)发现每个位置上三个圆圈中的数的和均为______________.由此可得,这三个三角形数阵所有圆圈中数的总和为:
3(![]() )=_________________.因此,
)=_________________.因此,![]() =__________.
=__________.

图2
[问题解决]
(1).根据以上规律可得![]() __________________.
__________________.
(2).试计算 ![]() ,请写出计算步骤.
,请写出计算步骤.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长方形纸条上画一条数轴.

(1)若折叠纸条,数轴上表示﹣3的点与表示5的点重合,则折痕与数轴的交点表示的数为 ;
(2)若将此纸条沿图中虚线处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折2次后,再将其展开,则最左端的折痕和最右端的折痕与数轴的交点表示的数分别是 ;
(3)如果该数轴上的两个点表示的数为a和b,经过对折,两点恰好重合,则折痕与数轴的交点表示的数为 ;(用含a,b的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com