
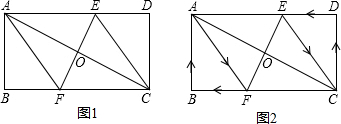
分析 (1)先证明四边形ABCD为平行四边形,再根据对角线互相垂直平分的平行四边形是菱形作出判定;
(2)根据勾股定理即可求AF的长;
(3)动点M、N分别从A、C两点同时出发,只有当M、N分别位于BE和DF上时,以A、M、C、N四点为顶点的四边形才能是平行四边形,根据MC∥AN,当MC=AN时,四边形AMCN是平行四边形,因为四边形AECF是菱形,所以MC=10tcm,AN=16+8-8t=(24-8t)cm,即10t=24-8t,解得:t=$\frac{4}{3}$,即可解答.
解答 解:(1)∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CAD=∠ACB,∠AEF=∠CFE,
∵EF垂直平分AC,
∴OA=OC,
∵在△AOE和△COF中,
$\left\{\begin{array}{l}{∠CAD=∠ACB}\\{∠AEF=∠CFE}\\{OA=OC}\end{array}\right.$,
∴△AOE≌△COF(AAS),
∴OE=OF(AAS),
∵EF⊥AC,
∴四边形AFCE为菱形;
(2)设菱形的边长AF=CF=xcm,则BF=(16-x)cm,
在Rt△ABF中,AB=8cm,由勾股定理,得:
64+(16-x)2=x2,
解得:x=10,
∴AF=10;
(3)∵动点M、N分别从A、C两点同时出发,
∴只有当M、N分别位于BE和DF上时,以A、M、C、N四点为顶点的四边形才能是平行四边形,
∵MC∥AN,
∴当MC=AN时,四边形AMCN是平行四边形,
∵四边形AECF是菱形,
∴MC=10tcm,AN=16+8-8t=(24-8t)cm,
∴10t=24-8t,
解得:t=$\frac{4}{3}$,
∴当t=$\frac{4}{3}$时,四边形AMCN是平行四边形.
点评 本题考查了矩形的性质的运用,菱形的判定及性质的运用,勾股定理的运用,平行四边形的判定及性质的运用,解答时分析清楚动点在不同的位置所构成的图形的形状是解答本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:填空题
已知关于x的方程kx2+(k+2) x+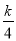 =0有两个不相等的实数根,则k的取值范围是__________.
=0有两个不相等的实数根,则k的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①④ | C. | ①②③ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
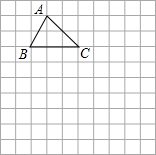 在10×10正方形的网格中,每个正方形的边长均为一个单位,将ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转180°,得到△A″B″C′,请画出△A′B′C′和△A″B″C′.(不写画法)
在10×10正方形的网格中,每个正方形的边长均为一个单位,将ABC向下平移4个单位,得到△A′B′C′,再把△A′B′C′绕点C′顺时针旋转180°,得到△A″B″C′,请画出△A′B′C′和△A″B″C′.(不写画法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com