
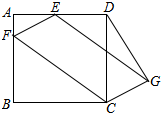
 如图,正方形ABCD的边长为4,点E是AD的中点,点F在AB上且AF=1,以EF、CF为边作平行四边形EFCG,连DG,则DG=$\sqrt{13}$.
如图,正方形ABCD的边长为4,点E是AD的中点,点F在AB上且AF=1,以EF、CF为边作平行四边形EFCG,连DG,则DG=$\sqrt{13}$. 分析 过G作GH⊥CD于H,由四边形EFCG是平行四边形,得到EF∥CG,由正方形的性质得到AB∥CD,推出∠EFC+∠FCD+∠DCG=∠AFE+∠EFC+∠FCD=180°,然后通过三角形全等证得AE=HG=2,CH=AF=1,从而得到结果.
解答 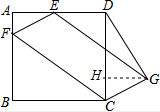 解;过G作GH⊥CD于H,
解;过G作GH⊥CD于H,
∵四边形EFCG是平行四边形,
∴EF∥CG,∵AB∥CD,
∴∠EFC+∠FCD+∠DCG=∠AFE+∠EFC+∠FCD=180°,
∴∠AFE=∠HCG,
在△AEF与△CHG中,
$\left\{\begin{array}{l}{∠A=∠GHC=90°}\\{∠AFE=∠HCG}\\{EF=CG}\end{array}\right.$,
∴△AEF≌△CHG,
∴AE=HG=2,CH=AF=1,
∴DH=3,
∴DG=$\sqrt{{3}^{3}{+2}^{2}}$=$\sqrt{13}$.
点评 本题考查了正方形的性质,平行四边形的性质,全等三角形的判定与性质,正确的作出辅助线是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2016-2017学年度海南省九年级第二次月考数学试卷(解析版) 题型:填空题
某校图书馆去年底有图书5万册,预计到明年年底增加到7.2万册,则这两年的年平均增长率为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
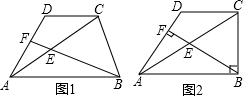 如图1,在梯形ABCD中,AB∥CD,AC=2CD,AB=nDC,E为对角线AC的中点.
如图1,在梯形ABCD中,AB∥CD,AC=2CD,AB=nDC,E为对角线AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
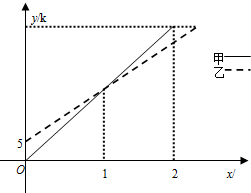 在一条直线上依次有A、B、C三地,自行车爱好者甲、乙两人同时分别从A、B两地出发,沿直线匀速骑向C地.已知甲的速度为20km/h,设甲、乙两人行驶x(h)后,与A地的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.两人在出发时都配备了通话距离为3km的对讲机,便于两人在骑车过程中可以用对讲机通话.下列说法:
在一条直线上依次有A、B、C三地,自行车爱好者甲、乙两人同时分别从A、B两地出发,沿直线匀速骑向C地.已知甲的速度为20km/h,设甲、乙两人行驶x(h)后,与A地的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.两人在出发时都配备了通话距离为3km的对讲机,便于两人在骑车过程中可以用对讲机通话.下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 各类 | 频数 | 频率 |
| 卡通画 | a | 0.56 |
| 时文杂志 | 32 | b |
| 武侠小说 | 30 | 0.15 |
| 文学名著 | c | d |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
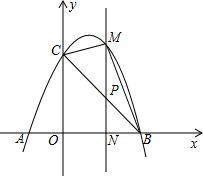 如图,已知抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
如图,已知抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com