
【题目】如图1,在平行四边形ABCD中,E,F分别在边AD,AB上,连接CE,CF,且满足∠DCE=∠BCF,BF=DE,∠A=60°,连接EF.
(1)若EF=2,求△AEF的面积;
(2)如图2,取CE的中点P,连接DP,PF,DF,求证:DP⊥PF.

【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】分析:(1)先证明△CDE≌△CBF,得到CD=CB,可得ABCD是菱形,则AD=AB,由DE=BF得AE=AF,则△AEF是等边三角形,根据EF的长可得△AEF的面积;
(2)延长DP交BC于N,连结FN,证明△CPN≌△EPD,得到AE=BN,证明△FBN≌△DEF,得到FN=FD,根据等腰三角形三线合一的性质可得结论.
详解:(1)∵四边形ABCD是平行四边形,
∴∠D=∠B,
∵BF=DE,∠DCE=∠BCF,
∴△CDE≌△CBF(AAS),
∴CD=CB,
∴ABCD是菱形,
∴AD=AB,
∴AD﹣DE=AB﹣BF,即AE=AF,
∵∠A=60°,
∴△AEF是等边三角形,
∵EF=2,
∴S△AEF=![]() ×22=
×22=![]() ;
;
(2)证明:如图2,延长DP交BC于N,连结FN,
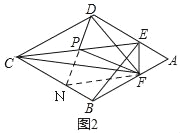
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠EDP=∠PNC,∠DEP=∠PCN,
∵点P是CE的中点,
∴CP=EP.
∴△CPN≌△EPD,
∴DE=CN,PD=PN.
又∵AD=BC.
∴AD﹣DE=BC﹣CN,即AE=BN.
∵△AEF是等边三角形,
∴∠AEF=60°,EF=AE.
∴∠DEF=120°,EF=BN.
∵AD∥BC,
∴∠A+∠ABC=180°,
又∵∠A=60°,
∴∠ABC=120°,
∴∠ABC=∠DEF.
又∵DE=BF,BN=EF.
∴△FBN≌△DEF,
∴DF=NF,
∵PD=PN,
∴PF⊥PD.


科目:初中数学 来源: 题型:
【题目】节能灯在城市已经基本普及,某商场计划购进甲、乙两种型号的节能灯共1200只,这两种节能灯的进价、售价如下表:
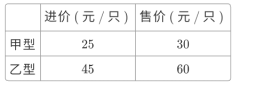
(1)如何进货,进货款恰好为46000元.
(2)如何进货,商场销售完节能灯后获利恰好是进货价的30%,此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东在研究数学问题时遇到一个定义:将三个已经排好顺序数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,![]() =
=![]() ,
,![]() =
=![]() ,所以数列2,-1,3的最佳值为
,所以数列2,-1,3的最佳值为![]() .
.
东东进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1,2,3的最佳值为![]() ;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列-4,-3,1的最佳值为
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OM是∠AOC的平分线.ON是∠BOC的平分线.
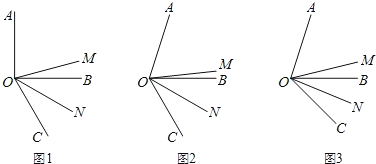
(1)如图1,当∠AOB=90°,∠BOC=60°时,∠MON的度数是多少?为什么?
(2)如图2,当∠AOB=70°,∠BOC=60°时,∠MON= (直接写出结果)
(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON﹣∠CON= (直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知A(![]() ,y1),B(2,y2)为反比例函数y=
,y1),B(2,y2)为反比例函数y=![]() 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )

A.(![]() ,0) B.(1,0) C.(
,0) B.(1,0) C.(![]() ,0) D.(
,0) D.(![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球训练中,为了训练球员快速抢断转身,教练设计了折返跑训练.教练在东西方向的足球场上画了一条直线插上不同的折返旗帜,如果约定向西为正,向东为负,练习一组的行驶记录如下(单位:米):+40,-30,+50,-25,+25,-30,+15,-28,+16,-20.
(1)球员最后到达的地方在出发点的哪个方向?距出发点多远?
(2)球员训练过程中,最远处离出发点多远?
(3)球员在一组练习过程中,跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为奖励学习之星,准备在某商店购买A、B两种文具作为奖品,已知一件A种文具的价格比一件B种文具的价格便宜5元,且用600元买A种文具的件数是用400元买B种文具的件数的2倍.
(1)求一件A种文具的价格;
(2)根据需要,该校准备在该商店购买A、B两种文具共150件.
①求购买A、B两种文具所需经费W与购买A种文具的件数a之间的函数关系式;
②若购买A种文具的件数不多于B种文具件数的2倍,且计划经费不超过2750元,求有几种购买方案,并找出经费最少的方案,及最少需要多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣![]() ,0),点B的坐标为(0,3).
,0),点B的坐标为(0,3).
(1)求过A,B两点直线的函数表达式;
(2)过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将口ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF
(2)若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com