
【题目】节能灯在城市已经基本普及,某商场计划购进甲、乙两种型号的节能灯共1200只,这两种节能灯的进价、售价如下表:
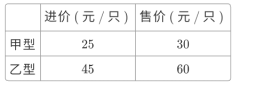
(1)如何进货,进货款恰好为46000元.
(2)如何进货,商场销售完节能灯后获利恰好是进货价的30%,此时利润为多少元?
【答案】(1)购进甲型节能灯400只,购进乙型节能灯800只,进货款恰好为46000元;
(2)购进甲型节能灯450只,购进乙型节能灯750只,销售完节能灯后利润为13500元.
【解析】
(1)设商场购进甲型节能灯![]() 只,则购进乙型节能灯
只,则购进乙型节能灯![]() 只,由题意可得等量关系:甲型的进货款+乙型的进货款=46000元,根据等量关系列出方程,再解方程即可;
只,由题意可得等量关系:甲型的进货款+乙型的进货款=46000元,根据等量关系列出方程,再解方程即可;
(2)设商场购进甲型节能灯![]() 只,则购进乙型节能灯
只,则购进乙型节能灯![]() 只,由题意可得:甲型的总利润+乙型的总利润=总进货款×30%,根据等量关系列出方程,再解即可.
只,由题意可得:甲型的总利润+乙型的总利润=总进货款×30%,根据等量关系列出方程,再解即可.
解:(1)设商场购进甲型节能灯![]() 只,则购进乙型节能灯
只,则购进乙型节能灯![]() 只
只
根据题意,得:![]()
解得:![]()
购进乙型节能灯为![]()
答:购进甲型节能灯400只,购进乙型节能灯800只,进货款恰好为46000元;
(2)设商场购进甲型节能灯![]() 只,则购进乙型节能灯
只,则购进乙型节能灯![]() 只,
只,
根据题意,得:![]() ,
,
解得:![]() ,
,
购进乙型节能灯为![]() ,
,
获利:![]() ,
,
答:购进甲型节能灯450只,购进乙型节能灯750只,销售完节能灯后利润为13500元.


科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,![]() ,将长方形ABCD绕点D逆时针旋转90°,点A、B、C分别对应点E、F、G.
,将长方形ABCD绕点D逆时针旋转90°,点A、B、C分别对应点E、F、G.
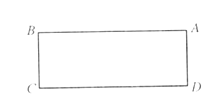
(1)画出长方形EFGD;
(2)连接BD、DF、BF,请用含有a、b的代数式表示![]() 的面积;
的面积;
(3)如果BF交CD于点H,请用含有a、b的代数式表示CH的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆准备购进一批换气扇,从电器商场了解到:一台A型换气扇和三台B型换气扇共需275元;三台A型换气扇和两台B型换气扇共需300元.
(1)求一台A型换气扇和一台B型换气扇的售价各是多少元;
(2)若该宾馆准备同时购进这两种型号的换气扇共80台,并且A型换气扇的数量不多于B型换气扇数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛,各参赛选手的成绩如下:
九(1)班:88,91,92,93,93,93,94,98,98,100;
九(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | m | 93 | 93 | 12 |
九(2)班 | 99 | 95 | n | p | 8.4 |
(1)直接写出表中m、n、p的值为:m=______,n=______,p=______;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好.”但也有人说(2)班的成绩要好.请给出两条支持九(2)班成绩更好的理由;
(3)学校确定了一个标准成绩,等于或大于这个成绩的学生被评定为“优秀”等级,如果九(2)班有一半的学生能够达到“优秀”等级,你认为标准成绩应定为______分,请简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+1与双曲线y=![]() 相交于P(1,m),Q(-2,-1)两点.
相交于P(1,m),Q(-2,-1)两点.
(1)求m的值;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上三点,且x1<x2<0<x3,请直接说明y1,y2,y3的大小关系;
(3)观察图象,请直接写出不等式k1x+1>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,∠OAB=90°,OA=AB=6,将
中,∠OAB=90°,OA=AB=6,将![]() 绕点O沿逆时针方向旋转90°得到
绕点O沿逆时针方向旋转90°得到![]() .
.
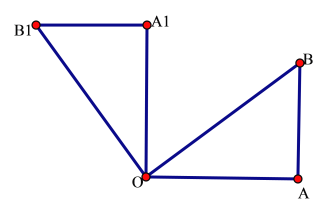
(1)线段![]() 的长是
的长是
(2)![]() 的度数是 ;
的度数是 ;
(3)求四边形的面积![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学玩“托球赛跑”游戏,商定:用球拍托着乒乓球从起跑线l起跑,绕过点P跑回到起跑线l(如图所示),途中乒乓球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果:甲同学由于心急,掉了球,浪费了6秒钟,乙同学则顺利跑完.事后,乙同学说:“我俩所用的全部时间的和为50秒,捡球过程不算在内时,甲的速度是我的1.2倍.”根据图文信息,请问哪位同学获胜?
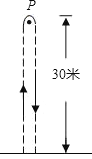
查看答案和解析>>
科目:初中数学 来源: 题型:
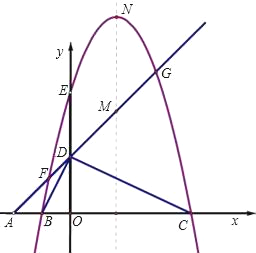
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平行四边形ABCD中,E,F分别在边AD,AB上,连接CE,CF,且满足∠DCE=∠BCF,BF=DE,∠A=60°,连接EF.
(1)若EF=2,求△AEF的面积;
(2)如图2,取CE的中点P,连接DP,PF,DF,求证:DP⊥PF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com