
【题目】某宾馆准备购进一批换气扇,从电器商场了解到:一台A型换气扇和三台B型换气扇共需275元;三台A型换气扇和两台B型换气扇共需300元.
(1)求一台A型换气扇和一台B型换气扇的售价各是多少元;
(2)若该宾馆准备同时购进这两种型号的换气扇共80台,并且A型换气扇的数量不多于B型换气扇数量的3倍,请设计出最省钱的购买方案,并说明理由.
【答案】(1)一台A型换气扇的售价为50元,一台B型换气扇的售价为75元;(2)最省钱的方案是购进60台A型换气扇,20台B型换气扇,理由见解析.
【解析】分析:(1)设一台A型换气扇的售价为x元,一台B型换气扇的售价为y元,列二元一次方程组求解;(2)设购进A型换气扇z台,总费用为w元,根据“A型换气扇的数量不多于B型换气扇数量的3倍,”,求z的取值范围,根据“同时购进这两种型号的换气扇共80台”求w与z的函数关系,由函数的性质确定方案.
详解:(1)设一台A型换气扇的售价为x元,一台B型换气扇的售价为y元.
根据题意得:![]() 解得:
解得:![]()
答:一台A型换气扇的售价为50元,一台B型换气扇的售价为75元.
(2)设购进A型换气扇z台,总费用为w元,
则有z≤3(80-z),解得:z≤60,
∵z为换气扇的台数,∴z≤60且z为正整数,
w=50z+75(80-z)=-25z+6000,
∵-25<0,∴w随着z的增大而减小,
∴当z=60时,w最大=25×60+6000=4500,
此时80-z=80-60=20.
答:最省钱的方案是购进60台A型换气扇,20台B型换气扇.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图),通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
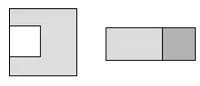
A.a2-b2=(a+b)(a-b)
B.(a+b)2=a2+2ab+b2
C.(a-b)2=a2-2ab+b2
D.a2-ab=a(a-b)
查看答案和解析>>
科目:初中数学 来源: 题型:
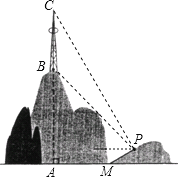
【题目】如图,山顶建有一座铁塔,塔高![]() 米,测量人员在一个小山坡的P处测得塔的底部B点的仰角为
米,测量人员在一个小山坡的P处测得塔的底部B点的仰角为![]() ,塔顶C点的仰角为
,塔顶C点的仰角为![]() 已测得小山坡的坡角为
已测得小山坡的坡角为![]() ,坡长
,坡长![]() 米
米![]() 求山的高度
求山的高度![]() 精确到1米
精确到1米![]() 参考数据:
参考数据:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
已知A、B两地相距48千米,甲骑自行车每小时走18千米,乙步行每小时走6千米,甲乙两人分别A、B两地同时出发.
(1)同向而行,开始时乙在前,经过多少小时甲追上乙?
(2)相向而行,经过多少小时两人相距40千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE,求证:四边形AFCE为菱形;
(2)如图2,若AB=4cm,AF=5cm,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中:
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为![]() 秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求
秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求![]() 的值;
的值;
②若点P、Q的运动路程分别为![]() (单位:cm,
(单位:cm,![]() ),已知A、C、P、Q四点为顶点的四边形是平行四边形,求
),已知A、C、P、Q四点为顶点的四边形是平行四边形,求![]() 与
与![]() 满足的数量关系式。
满足的数量关系式。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=12,BC=9,点E,G分别为边AB,AD上的点,若矩形AEFG与矩形ABCD相似,且相似比为![]() ,连接CF,则CF= .
,连接CF,则CF= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+5x﹣2m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若两个实数根分别为x1和x2,且x12+x22=23,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节能灯在城市已经基本普及,某商场计划购进甲、乙两种型号的节能灯共1200只,这两种节能灯的进价、售价如下表:
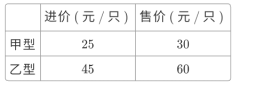
(1)如何进货,进货款恰好为46000元.
(2)如何进货,商场销售完节能灯后获利恰好是进货价的30%,此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东在研究数学问题时遇到一个定义:将三个已经排好顺序数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,![]() =
=![]() ,
,![]() =
=![]() ,所以数列2,-1,3的最佳值为
,所以数列2,-1,3的最佳值为![]() .
.
东东进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1,2,3的最佳值为![]() ;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列-4,-3,1的最佳值为
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com