练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】列方程解应用题：

    已知A、B两地相距48千米，甲骑自行车每小时走18千米，乙步行每小时走6千米，甲乙两人分别A、B两地同时出发．

    （1）同向而行，开始时乙在前，经过多少小时甲追上乙？

    （2）相向而行，经过多少小时两人相距40千米？

    【答案】（1）同向而行，开始时乙在前，经过4小时甲追上乙；（2）相向而行，经过小时或小时两人相距40千米．

    【解析】

    （1）根据题意可以列出相应的方程，本题得以解决；
    （2）根据题意，分两种情况，一种是相遇前相距40千米，一种是相遇后相距40千米，从而可以分别写出两种情况下的方程，本题得以解决．

    （1）设同向而行，开始时乙在前，经过x小时甲追上乙，

    18x﹣6x＝48

    解得，x＝4

    即同向而行，开始时乙在前，经过4小时甲追上乙；

    （2）设相向而行，经过x小时两人相距40千米，

    18x+6x＝48﹣40或18x+6x＝48+40，

    解得x＝或x＝

    即相向而行，经过小时或小时两人相距40千米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

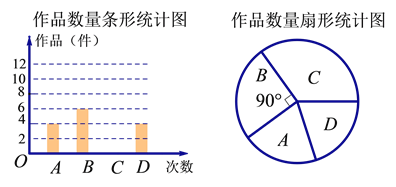
    【题目】某中学艺术节期间，学校向学生征集书画作品，学校从全校30个班中随机抽取了4个班 (用A，B，C，D表示)，对征集到的作品的数量进行了分析统计，制作了两幅不完整的统计图．请根据以上信息，回答下列问题：

    （1）请你将条形统计图补充完整，并估计全校共征集多少件作品？

    （2）如果全校征集的作品中有5件获得一等奖，其中有3名作者是男生，2名作者是女生，现要在获得一等奖的作者中选取两人参加表彰座谈会，请你用列表或树状图的方法，求恰好选取的两名学生性别相同的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长方形ABCD中，，将长方形ABCD绕点D逆时针旋转90°，点A、B、C分别对应点E、F、G.

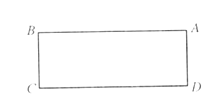
    (1)画出长方形EFGD;

    (2)连接BD、DF、BF，请用含有a、b的代数式表示的面积;

    (3)如果BF交CD于点H，请用含有a、b的代数式表示CH的长度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知矩形ABCD的三个顶点、、抛物线过A、C两点．

    直接写出点A的坐标，并求出抛物线的解析式；

    动点P从点A出发沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD向终点D运动速度均为每秒1个单位长度，运动时间为t秒过点P作交AC于点E．

    过点E作于点F，交抛物线于点当t为何值时，线段EG最长？

    连接在点P、Q运动的过程中，判断有几个时刻使得是等腰三角形？请直接写出相应的t值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

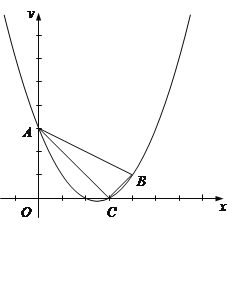
    【题目】已知抛物线经过点、、．

    （1）求抛物线的解析式；

    （2）联结AC、BC、AB，求的正切值；

    （3）点P是该抛物线上一点，且在第一象限内，过点P作交轴于点，当点在点的上方，且与相似时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

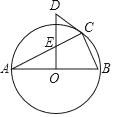
    【题目】如图，△ABC内接于⊙O，且AB为⊙O的直径OD⊥AB，与AC交于点E，与过点C的⊙O切线交于点D．

    （1）若AC=6，BC=3，求OE的长．

    （2）试判断∠A与∠CDE的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某宾馆准备购进一批换气扇,从电器商场了解到:一台A型换气扇和三台B型换气扇共需275元;三台A型换气扇和两台B型换气扇共需300元.

    (1)求一台A型换气扇和一台B型换气扇的售价各是多少元;

    (2)若该宾馆准备同时购进这两种型号的换气扇共80台,并且A型换气扇的数量不多于B型换气扇数量的3倍,请设计出最省钱的购买方案,并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校九年级两个班，各选派10名学生参加学校举行的“汉字听写”大赛预赛，各参赛选手的成绩如下：

    九(1)班：88，91，92，93，93，93，94，98，98，100；

    九(2)班：89，93，93，93，95，96，96，98，98，99．

    通过整理，得到数据分析表如下：

    班级

    最高分

    平均分

    中位数

    众数

    方差

    九(1)班

    100

    m

    93

    93

    12

    九(2)班

    99

    95

    n

    p

    8.4

    (1)直接写出表中m、n、p的值为：m=______，n=______，p=______；

    (2)依据数据分析表，有人说：“最高分在(1)班，(1)班的成绩比(2)班好．”但也有人说(2)班的成绩要好．请给出两条支持九(2)班成绩更好的理由；

    (3)学校确定了一个标准成绩，等于或大于这个成绩的学生被评定为“优秀”等级，如果九(2)班有一半的学生能够达到“优秀”等级，你认为标准成绩应定为______分，请简要说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

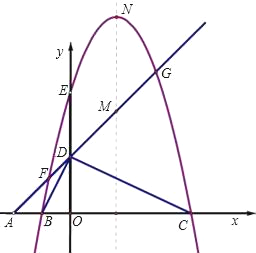
    【题目】如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，B为线段OA的中点，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M，点P为线段FG上一个动点（与F、G不重合），PQ∥y轴与抛物线交于点Q．

    （1）求经过B、E、C三点的抛物线的解析式；

    （2）判断△BDC的形状，并给出证明；当P在什么位置时，以P、O、C为顶点的三角形是等腰三角形，并求出此时点P的坐标；

    （3）若抛物线的顶点为N，连接QN，探究四边形PMNQ的形状：①能否成为菱形；②能否成为等腰梯形？若能，请直接写出点P的坐标；若不能，请说明理由．

    查看答案和解析>>

    同步练习册答案