
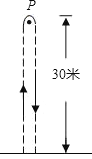
【题目】甲、乙两同学玩“托球赛跑”游戏,商定:用球拍托着乒乓球从起跑线l起跑,绕过点P跑回到起跑线l(如图所示),途中乒乓球掉下时须捡起并回到掉球处继续赛跑,用时少者胜.结果:甲同学由于心急,掉了球,浪费了6秒钟,乙同学则顺利跑完.事后,乙同学说:“我俩所用的全部时间的和为50秒,捡球过程不算在内时,甲的速度是我的1.2倍.”根据图文信息,请问哪位同学获胜?
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
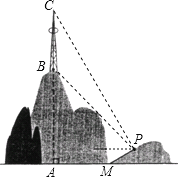
【题目】如图,山顶建有一座铁塔,塔高![]() 米,测量人员在一个小山坡的P处测得塔的底部B点的仰角为
米,测量人员在一个小山坡的P处测得塔的底部B点的仰角为![]() ,塔顶C点的仰角为
,塔顶C点的仰角为![]() 已测得小山坡的坡角为
已测得小山坡的坡角为![]() ,坡长
,坡长![]() 米
米![]() 求山的高度
求山的高度![]() 精确到1米
精确到1米![]() 参考数据:
参考数据:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+5x﹣2m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若两个实数根分别为x1和x2,且x12+x22=23,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节能灯在城市已经基本普及,某商场计划购进甲、乙两种型号的节能灯共1200只,这两种节能灯的进价、售价如下表:
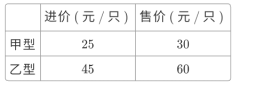
(1)如何进货,进货款恰好为46000元.
(2)如何进货,商场销售完节能灯后获利恰好是进货价的30%,此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若干名工人某天生产同一种玩具,生产的玩具数整理成条形图(如图所示).则他们生产的玩具数的平均数、中位数、众数分别为( )

A.5,5,4 B.5,5,5
C.5,4,5 D.5,4,4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用正方形是墩垒石梯,下图分别表示垒到一、二阶梯时的情况,那么照这样垒下去
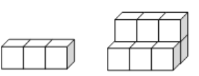
一级 二级
①填出下表中未填的两空,观察规律。
阶梯级数 | 一级 | 二级 | 三级 | 四级 |
石墩块数 | 3 | 9 |
②到第n级阶梯时,共用正方体石墩_______________块(用n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读下面材料:
点A,B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|.
当A,B两点中有一点在原点时,不妨设点A在原点,如图(1),|AB|=|OB|=|b|=|a﹣b|;当A,B两点都不在原点时,
①如图(2),点A,B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|;
②如图(3),点A,B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=|a﹣b|;
③如图(4),点A,B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=|a﹣b|;
综上,数轴上A,B两点之间的距离|AB|=|a﹣b|.
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示1和﹣3的两点之间的距离是 ;
②数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2,那么x为 ;
③当代数式|x+1|+|x﹣2|取最小值时,相应的x的取值范围是 .
④解方程|x+1|+|x﹣2|=5.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东在研究数学问题时遇到一个定义:将三个已经排好顺序数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,![]() =
=![]() ,
,![]() =
=![]() ,所以数列2,-1,3的最佳值为
,所以数列2,-1,3的最佳值为![]() .
.
东东进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1,2,3的最佳值为![]() ;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
;数列3,-1,2的最佳值为1;….经过研究,东东发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列-4,-3,1的最佳值为
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为 ,取得最佳值最小值的数列为 (写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为奖励学习之星,准备在某商店购买A、B两种文具作为奖品,已知一件A种文具的价格比一件B种文具的价格便宜5元,且用600元买A种文具的件数是用400元买B种文具的件数的2倍.
(1)求一件A种文具的价格;
(2)根据需要,该校准备在该商店购买A、B两种文具共150件.
①求购买A、B两种文具所需经费W与购买A种文具的件数a之间的函数关系式;
②若购买A种文具的件数不多于B种文具件数的2倍,且计划经费不超过2750元,求有几种购买方案,并找出经费最少的方案,及最少需要多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com