
【题目】计算:(1)已知x﹣2的平方根是±4,2x﹣y+12的立方根是4,求![]() 的值;
的值;
(2)在Rt△ABC中,∠C=90°,若c=10cm,a:b=3:4,求△ABC的周长;
(3)已知a=![]() ,b=
,b=![]() ,试求a2+b2、a2+3ab+b2的值.
,试求a2+b2、a2+3ab+b2的值.
【答案】(1)1156;(2)24cm;(3)![]() ,
,![]() .
.
【解析】
(1)根据平方根的性质和立方根的性质得出x-2=16,2x-y+12=64,求出x和y的值,再代入计算即可;
(2)设a=3xcm,b=4xcm,由勾股定理得出方程,解方程求出x,得出a和b,即可得出结果.
(3)先化简a=![]() =2﹣
=2﹣![]() ,b=
,b=![]() =2+
=2+![]() ,再把a,b代入即可解答.
,再把a,b代入即可解答.
解:(1)∵x﹣2的平方根是±4,2x﹣y+12的立方根是4,
∴x﹣2=16,2x﹣y+12=64,
∴x=18,y=﹣16,
∴(x﹣y)x+y=342=1156;
(2)设a=3xcm,b=4xcm,
∵∠C=90°,
∴(3x)2+(4x)2=102,
解得:x=2,
∴a=6,b=8,
∴△ABC的周长=a+b+c=6+8+10=24(cm);
(3)∵a=![]() =2﹣
=2﹣![]() ,b=
,b=![]() =2+
=2+![]() ,
,
∴a2+b2=7﹣4![]() +7+4
+7+4![]() =14;
=14;
a2+3ab+b2=7﹣4![]() +7+4
+7+4![]() +3×1=17.
+3×1=17.


科目:初中数学 来源: 题型:
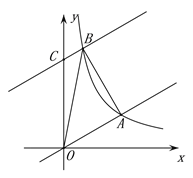
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x与反比例函数y=k/x在第一象限内的图象相交于点A(m,3).
x与反比例函数y=k/x在第一象限内的图象相交于点A(m,3).
(1)求该反比例函数的关系式;
(2)将直线y=![]() x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
(3)在(2)的条件下,在射线OA上存在一点P,使△PAB∽△BAO,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
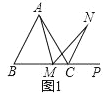
【题目】如图1所示,(1)在正三角形ABC中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠ACP的平分线上一点,若∠AMN=60°,求证:AM=MN.
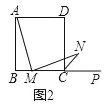
(2)若将(1)中“正三角形ABC”改为“正方形ABCD”,N是∠DCP的平分线上一点,若∠AMN=90°,则AM=MN是否成立?若成立,请证明;若不成立,说明理由.
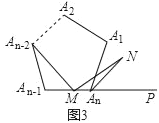
(3)若将(2)中的“正方形ABCD”改为“正n边形A1A2…An“,其它条件不变,请你猜想:当∠An﹣2MN=_____°时,结论An﹣2M=MN仍然成立.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
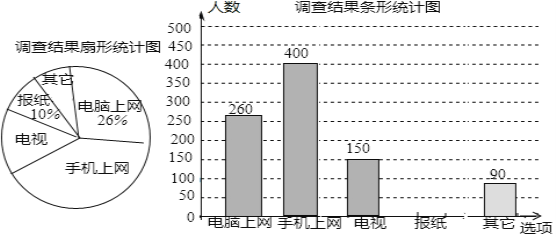
根据以上信息解答下列问题.
(1)这次抽样调查的样本容量是__________.
(2)通过“电视”了解新闻的人数占被调查人数的百分比为______;扇形统计图中,“手机上网”所对应的圆心角的度数是_________.
(3)请补全条形统计图;
(4)若该市约有950万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点P是正方形ABCD内的一点,连PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图1).
①设AB的长为a,PB的长为b(b<a),求△PAB旋转到△P′CB的过程中边PA所扫过区域(图1中阴影部分)的面积;
②若PA=2,PB=4,∠APB=135°,求PC的长.
(2)如图2,若PA2+PC2=2PB2,请说明点P必在对角线AC上.
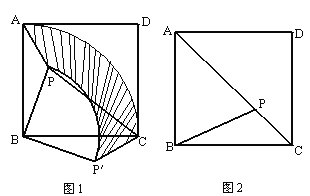
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生开展课外社会实践活动,现有甲、乙两种大客车可租,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,甲种客车每辆载客量45人,乙种客车每辆载客量30人,共有师生330人,求最节省的租车费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列方程:①![]() ;②0.3x=1;③
;②0.3x=1;③![]() ;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的个数是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
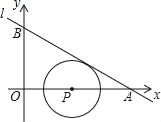
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初二学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:
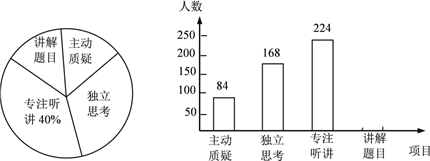
(1)在这次评价中,一共抽查了 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初二学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com