
����Ŀ��ijУ��֯ѧ����չ�������ʵ��������мס������ִ�ͳ����⣬��֪1�����ֿͳ���3�����ֿͳ��������1240Ԫ��3�����ֿͳ���2�����ֿͳ��������1760Ԫ��
��1����1�����ֿͳ���1�����ֿͳ������ֱ��Ƕ���Ԫ��
��2��ѧУ�ƻ����üס������ֿͳ���8�������ֿͳ�ÿ���ؿ���45�ˣ����ֿͳ�ÿ���ؿ���30�ˣ�����ʦ��330�ˣ������ʡ��������Ƕ���Ԫ��
���𰸡�(1)�ͳ����ÿ��400Ԫ���ҿͳ����ÿ��280Ԫ��2�����ʡ���������2960Ԫ
����������1������ͳ����ÿ��xԪ���ҿͳ����ÿ��yԪ�����ݵ�����ϵ����1�����ֿͳ���3�����ֿͳ��������1240Ԫ����3�����ֿͳ���2�����ֿͳ��������1760Ԫ���г���������⼴����
��2����ͳ�����x�������ҿͳ����ˣ�8-x�������������ΪWԪ������W=�ͳ����+�ҿͳ�������ͳ��ؿ���+�ҿͳ��ؿ�����330�в���ʽ��������⼴�ɣ�
(1) ��ͳ����ÿ��xԪ���ҿͳ����ÿ��yԪ����������ã�
![]() ��
��
��ã�![]() ��
��
�𣺼ͳ����ÿ��400Ԫ���ҿͳ����ÿ��280Ԫ��
��2����ͳ�����x�������ҿͳ����ˣ�8-x�������������ΪWԪ����������ã�
W=400x+280(8-x)=2240+120x
45x+30(8-x)��330��
��ã�x��6��W��x�����������x=6ʱW��С��400��6+2��280=2960��
�����ʡ���������2960Ԫ��


 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�AB=6��AD=9����BAD��ƽ���߽�BC��E����DC���ӳ�����F��BG��AE��G��BG=![]() ������EFC���ܳ�Ϊ_____________.
������EFC���ܳ�Ϊ_____________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
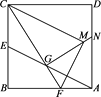
����Ŀ����������ABCD�У�AB=![]() ��E�DZ�BC���е㣬F��AB��һ�㣬�߶�AE��CF���ڵ�G����CE=EG����ABF��CF���ۣ�ʹ�õ�B���ڵ�M������GM���ӳ���AD�ڵ�N����AGN�����Ϊ_________________��
��E�DZ�BC���е㣬F��AB��һ�㣬�߶�AE��CF���ڵ�G����CE=EG����ABF��CF���ۣ�ʹ�õ�B���ڵ�M������GM���ӳ���AD�ڵ�N����AGN�����Ϊ_________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
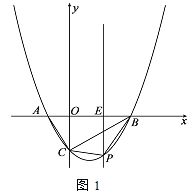
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C��
��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C��
��1���ж�ABC����״����˵�����ɣ�
��2����ͼ1����PΪֱ��BC�·��Ķ��κ���ͼ���ϵ�һ�����㣨��P��B��C���غϣ�������P��y���ƽ���߽�x���ڵ�E����PBC��������ֵʱ����FΪ�߶�BCһ�㣨����㡢�غϣ�������EF������G�ӵ�E���������߶�EF��ÿ��1����λ���ٶ��˶�����F������FC��ÿ��![]() ����λ���ٶ��˶�����C��ֹͣ������F�������Ƕ���ʱ����G�������˶���������ʱ���٣�
����λ���ٶ��˶�����C��ֹͣ������F�������Ƕ���ʱ����G�������˶���������ʱ���٣�
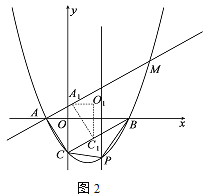
��3����ͼ2����ACO������CB������ÿ��![]() ����λ���ٶ�ƽ�ƣ���ƽ�ƺ��ACOΪA1C1O1������A A1,ֱ��A A1�����������M����ƽ�Ƶ�ʱ��Ϊt�룬��A MC1Ϊ����������ʱ����t��ֵ��
����λ���ٶ�ƽ�ƣ���ƽ�ƺ��ACOΪA1C1O1������A A1,ֱ��A A1�����������M����ƽ�Ƶ�ʱ��Ϊt�룬��A MC1Ϊ����������ʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺��1����֪x��2��ƽ��������4��2x��y+12����������4����![]() ��ֵ��
��ֵ��
��2����Rt��ABC�У���C��90������c��10cm��a��b��3��4������ABC���ܳ���
��3����֪a��![]() ��b��
��b��![]() ������a2+b2��a2+3ab+b2��ֵ��
������a2+b2��a2+3ab+b2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
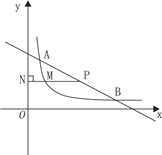
����Ŀ����ͼ��ֱ��![]() ��˫����
��˫����![]() ����A��B���㣬A��ĺ�����Ϊ2.
����A��B���㣬A��ĺ�����Ϊ2.
��1�����B�����ꣻ
��2��PΪ�߶�AB��һ�㣨�������˵㣩��P���������Ϊa����PN��y�ᣬ����ΪN����˫�����ڵ�M����![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ��A��B�Ǻ�l�����������ׯ����Ҫ�ں�l����һ����ˮվC��ʹ����A��B����ׯ�ľ���ĺ���С������ͼ�л�����C��λ�ã���������ͼ�ۼ���

��̽����
��2����ͼ��C��B������ׯ��һ����ֱ����·�����ˣ���ׯA����·�⣬Ҫ����·�Ͻ�һ������վO��ʹ��AO+BO+CO��С������ͼ�л�����O��λ�ã�
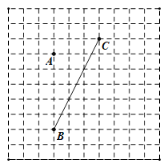
��3����ͼ������A��B��C��D�ĸ���ׯ�����Ҫ��һ������վO��ʹ��AO+BO+CO+DO��С������ͼ�л�����O��λ�ã�
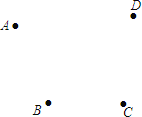
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
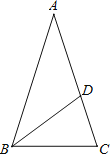
����Ŀ����ͼ��������ABC�У�AB=AC����BAC=36����BC=1����D�ڱ�AC����BDƽ����ABC����CD=x��
��1����֤����ABC�ס�BCD��
��2����x��ֵ��
��3����cos36��-cos72����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ʮ¹���ᣬС������¹����������¹�����Ἰ�Σ����ı��ԡ������㾭����������Ϊ������50ֻ¹��Ȧ�ᣬСȦ���������4ͷ¹����Ȧ���������6ͷ¹��������Ȧ��ļ�������õĽ���У� ��
A.3��B.4��C.5��D.6��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com