
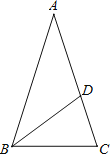
【题目】如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
(1)求证:△ABC∽△BCD;
(2)求x的值;
(3)求cos36°-cos72°的值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)由等腰三角形ABC中,顶角的度数求出两底角度数,再由BD为角平分线求出∠DBC的度数,得到∠DBC=∠A,再由∠C为公共角,利用两对角相等的三角形相似得到三角形ABC与三角形BCD相似;
(2)根据(1)结论得到AD=BD=BC,根据AD+DC表示出AC,由(1)两三角形相似得比例求出x的值即可;
(3)过B作BE垂直于AC,交AC于点E,在直角三角形ABE和直角三角形BCE中,利用锐角三角函数定义求出cos36°与cos72°的值,代入原式计算即可得到结果.
试题解析:(1)∵等腰△ABC中,AB=AC,∠BAC=36°,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∵∠CBD=∠A=36°,∠C=∠C,
∴△ABC∽△BCD;
(2)∵∠A=∠ABD=36°,
∴AD=BD,
∵BD=BC,
∴AD=BD=CD=1,
设CD=x,则有AB=AC=x+1,
∵△ABC∽△BCD,
∴![]() ,即
,即![]() ,
,
整理得:x2+x-1=0,
解得:x1=![]() ,x2=
,x2=![]() (负值,舍去),
(负值,舍去),
则x=![]() ;
;
(3)过B作BE⊥AC,交AC于点E,
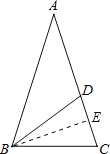
∵BD=CD,
∴E为CD中点,即DE=CE=![]() ,
,
在Rt△ABE中,cosA=cos36°=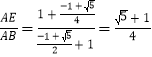 ,
,
在Rt△BCE中,cosC=cos72°=![]() ,
,
则cos36°-cos72°=![]() -
-![]() =
=![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,平面上有射线![]() 和点
和点![]() ,
,![]() ,请用尺规按下列要求作图:
,请用尺规按下列要求作图:
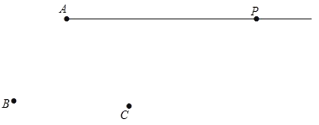
(1)连接![]() ,并在射线
,并在射线![]() 上截取
上截取![]() ;
;
(2)连接![]() 、
、![]() ,并延长
,并延长![]() 到
到![]() ,使
,使![]()
(3)在(2)的基础上,取![]() 中点
中点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生开展课外社会实践活动,现有甲、乙两种大客车可租,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,甲种客车每辆载客量45人,乙种客车每辆载客量30人,共有师生330人,求最节省的租车费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,E,C,F在同一条直线上,AB=DE,∠B=∠DEF.要使△ABC≌△DEF,则需要再添加的一个条件是_______.(写出一个即可)
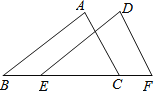
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
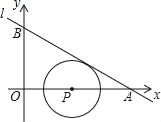
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上一点,且AD∥OC
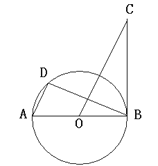
(1)求证:△ADB∽△OBC;
(2)若AB=2,BC=![]() ,求AD的长(结果保留根号).
,求AD的长(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
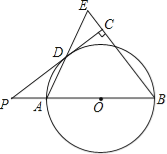
(1)求证:AB=BE;
(2)若PA=2,cosB=![]() ,求⊙O半径的长.
,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“水是生命之源”,某市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
月用水量(吨) | 单价(元/吨) |
不超过25吨 | 1.4 |
超过25吨的部分 | 2.1 |
另:每吨用水加收0.95元的城市污水处理费 | |
(1)如果1月份小明家用水量为18吨,那么小明家1月份应该缴纳水费 元;
(2)小明家2月份共缴纳水费104.5元,那么小明家2月份用水多少吨?
(3)小明家的水表3月份出了故障,只有80%的用水量记入水表中,这样小明家在3月份只缴纳了56.4元水费,问小明家3月份实际应该缴纳水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
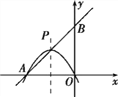
【题目】如图所示,直线y=![]() +3与x轴、y轴分别交于A、B两点,P是线段AB的中点,抛物线y=-
+3与x轴、y轴分别交于A、B两点,P是线段AB的中点,抛物线y=-![]() x2+bx+c经过点A,P,O(原点).
x2+bx+c经过点A,P,O(原点).
(1)求抛物线的表达式;
(2)在x轴上方的抛物线上是否存在一点Q,使∠QAO=45°?如果存在,求出Q点的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com