
【题目】(10分)如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
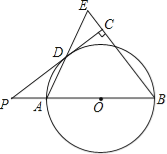
(1)求证:AB=BE;
(2)若PA=2,cosB=![]() ,求⊙O半径的长.
,求⊙O半径的长.
【答案】(1)见解析;(2)3
【解析】
试题(1)连接OD,由PD切⊙O于点D,得到OD⊥PD,由于BE⊥PC,得到OD∥BE,得出∠ADO=∠E,根据等腰三角形的性质和等量代换可得结果;
(2)由(1)知,OD∥BE,得到∠POD=∠B,根据三角函数的定义即可得到结果.
试题解析:(1)证明:连接OD,

∵PD切⊙O于点D,
∴OD⊥PD,
∵BE⊥PC,
∴OD∥BE,
∴∠ADO=∠E,
∵OA=OD,
∴∠OAD=∠ADO,
∴∠OAD=∠E,
∴AB=BE;
(2)解:由(1)知,OD∥BE,
∴∠POD=∠B,
∴cos∠POD=cosB=![]() ,
,
在Rt△POD中,cos∠POD=![]() ,
,
∵OD=OA,PO=PA+OA=2+OA,
∴![]() ,
,
∴OA=3,
∴⊙O半径=3.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
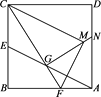
【题目】在正方形ABCD中,AB=![]() ,E是边BC的中点,F是AB上一点,线段AE、CF交于点G,且CE=EG,将ABF沿CF翻折,使得点B落在点M,连接GM并延长交AD于点N,则AGN的面积为_________________.
,E是边BC的中点,F是AB上一点,线段AE、CF交于点G,且CE=EG,将ABF沿CF翻折,使得点B落在点M,连接GM并延长交AD于点N,则AGN的面积为_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,A、B是河l两侧的两个村庄.现要在河l上修建一个抽水站C,使它到A、B两村庄的距离的和最小,请在图中画出点C的位置,并保留作图痕迹.

(探索)
(2)如图,C、B两个村庄在一条笔直的马路的两端,村庄A在马路外,要在马路上建一个垃圾站O,使得AO+BO+CO最小,请在图中画出点O的位置.
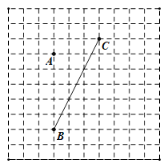
(3)如图,现有A、B、C、D四个村庄,如果要建一个垃圾站O,使得AO+BO+CO+DO最小,请在图中画出点O的位置.
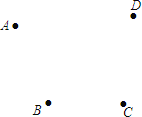
查看答案和解析>>
科目:初中数学 来源: 题型:
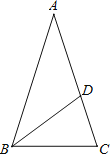
【题目】如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
(1)求证:△ABC∽△BCD;
(2)求x的值;
(3)求cos36°-cos72°的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把一根细线绳对折成两条重合的线段![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.

(l)若细线绳的长度是![]() ,求图中线段
,求图中线段![]() 的长;
的长;
(2)从点![]() 处把细线绳剪断后展开,细线绳变成三段,若三段中最长的一段为
处把细线绳剪断后展开,细线绳变成三段,若三段中最长的一段为![]() ,求原来细线绳的长.
,求原来细线绳的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点
上的一个动点![]() ,点
,点![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.

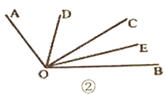
(1)若点![]() 恰好是
恰好是![]() 的中点,则
的中点,则![]() _______
_______![]() ;若
;若![]() ,则
,则![]() _________
_________![]() ;
;
(2)随着点![]() 位置的改版,
位置的改版,![]() 的长是否会改变?如果改变,请说明原因;如果不变,请求出的长;
的长是否会改变?如果改变,请说明原因;如果不变,请求出的长;
(3)知识迁移:如图②,已知![]() ,过角的内部任意一点
,过角的内部任意一点![]() 画射线
画射线![]() ,若
,若![]() 分别平分
分别平分![]() 和
和![]() ,试说明
,试说明![]() 的度数与射线
的度数与射线![]() 的位置无关.
的位置无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
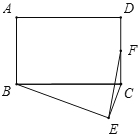
A. 8B. 9C. 10D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有五十鹿进舍,小舍容四鹿,大舍容六鹿,需舍几何?(改编自《缉古算经》)”大意为:今有50只鹿进圈舍,小圈舍可以容纳4头鹿,大圈舍可以容纳6头鹿,求所需圈舍的间数.求得的结果有( )
A.3种B.4种C.5种D.6种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中描出下列各组点,并将各组的点用线段依次连结起来.
(1)(1,0)、(6,0)、(6,1)、(5,0)、(6,-1)、(6,0);
(2)(2,0)、(5,3)、(4,0);
(3)(2,0)、(5,-3)、(4,0).
观察所得到的图形像什么?如果要将此图形向上平移到x轴上方,那么至少要向上平移几个单位长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com