
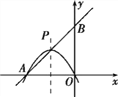
【题目】如图所示,直线y=![]() +3与x轴、y轴分别交于A、B两点,P是线段AB的中点,抛物线y=-
+3与x轴、y轴分别交于A、B两点,P是线段AB的中点,抛物线y=-![]() x2+bx+c经过点A,P,O(原点).
x2+bx+c经过点A,P,O(原点).
(1)求抛物线的表达式;
(2)在x轴上方的抛物线上是否存在一点Q,使∠QAO=45°?如果存在,求出Q点的坐标;如果不存在,请说明理由.
【答案】(1)抛物线的表达式为y=-![]() x2-
x2-![]() x;(2)存在,Q点的坐标为
x;(2)存在,Q点的坐标为![]() .
.
【解析】(1)根据直线AB的解析式,可求得B点坐标,而P为线段AB的中点,那么点P的纵坐标为B点纵坐标的一半,由于抛物线经过原点,那么c=0,根据公式法表示出P点纵坐标,即可求得b的值,由此确定该抛物线的解析式.(2)此题应分两种情况讨论:①当Q点在x轴上方时,由于∠OAQ=45°,那么直线AQ的斜率为k=1,而A点坐标易求得,即可得到直线AQ的解析式,联立抛物线的解析式,即可求得Q点坐标;
②当Q点在x轴下方时,方法同①.
(1)直线y=![]() +3与x轴、y轴分别交于点A,B,且P为线段AB的中点,抛物线y=-
+3与x轴、y轴分别交于点A,B,且P为线段AB的中点,抛物线y=-![]() x2+bx+c过A,P,O三点,
x2+bx+c过A,P,O三点,
∴OB=3,c=0,P必为抛物线的顶点,
∴![]() =
=![]() ,∴b=±
,∴b=±![]() .
.
又∵x=-![]() =
=![]() <0,∴b<0,∴b=-
<0,∴b<0,∴b=-![]() .
.
∴抛物线的表达式为y=-![]() x2-
x2-![]() x.
x.
(2)存在.
∵抛物线y=-![]() x2-
x2-![]() x经过点A,
x经过点A,
∴A点的坐标为(-4,0).
设Q点的坐标为(x,y),∵∠QAO=45°,
∴x=-4+y.
将其代入抛物线的关系式中得y=-![]() (-4+y)2-
(-4+y)2-![]() (-4+y),解得y1=0(舍去),y2=
(-4+y),解得y1=0(舍去),y2=![]() .
.
当y=![]() 时,x=-
时,x=-![]() .
.
∴Q点的坐标为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
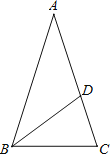
【题目】如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
(1)求证:△ABC∽△BCD;
(2)求x的值;
(3)求cos36°-cos72°的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有五十鹿进舍,小舍容四鹿,大舍容六鹿,需舍几何?(改编自《缉古算经》)”大意为:今有50只鹿进圈舍,小圈舍可以容纳4头鹿,大圈舍可以容纳6头鹿,求所需圈舍的间数.求得的结果有( )
A.3种B.4种C.5种D.6种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,给正五边形的顶点依次编号为![]() .若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.
.若从某一顶点开始,沿正五边形的边顺时针行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.
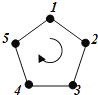
如:小宇同学从编号为![]() 的顶点开始,他应走
的顶点开始,他应走![]() 个边长,即从
个边长,即从![]() 为第一次“移位”,这时他到达编号为
为第一次“移位”,这时他到达编号为![]() 的顶点;然后从
的顶点;然后从![]() 为第二次“移位”,....若小宇同学从编号为
为第二次“移位”,....若小宇同学从编号为![]() 的顶点开始,则第九十九次“移位”后他所处顶点的编号是( )
的顶点开始,则第九十九次“移位”后他所处顶点的编号是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分9分)如图,以⊿ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且![]() .
.
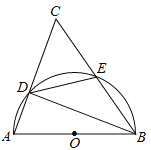
(1)试判断⊿ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励居民节约用水,某市自来水公司按如下方式对每户月用水量进行计算:当用水量不超过![]() 吨时,每吨的收费标准相同,当用水量超过
吨时,每吨的收费标准相同,当用水量超过![]() 吨时,超出
吨时,超出![]() 吨的部分每吨的收费标准也相同,下表是小明家
吨的部分每吨的收费标准也相同,下表是小明家![]() 月份用水量和交费情况:
月份用水量和交费情况:
月份 |
|
|
|
|
用水量(吨) |
|
|
|
|
费用(元) |
|
|
|
|
请根据表格中提供的信息,回答以下问题:
(1)若小明家![]() 月份用水量为
月份用水量为![]() 吨,则应缴水费________元;
吨,则应缴水费________元;
(2)若某户某月用了![]() 吨水(
吨水(![]() ),应付水费________元;
),应付水费________元;
(3)若小明家![]() 月份交纳水费
月份交纳水费![]() 元,则小明家
元,则小明家![]() 月份用水多少吨?
月份用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中描出下列各组点,并将各组的点用线段依次连结起来.
(1)(1,0)、(6,0)、(6,1)、(5,0)、(6,-1)、(6,0);
(2)(2,0)、(5,3)、(4,0);
(3)(2,0)、(5,-3)、(4,0).
观察所得到的图形像什么?如果要将此图形向上平移到x轴上方,那么至少要向上平移几个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
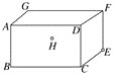
【题目】长方体敞口玻璃罐,长、宽、高分别为16 cm、6 cm和6 cm,在罐内点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形ABCD中心的正上方2 cm处,则蚂蚁到达饼干的最短距离是多少cm.( )
A. 7![]() B.
B. ![]()
C. 24D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把2018个正整数1,2,3,4,…,2018按如图方式排列成一个表.

(1)用如图方式框住表中任意4个数,记左上角的一个数为![]() ,则另三个数用含
,则另三个数用含![]() 的式子表示出来,从小到大依次是__________、___________、_______________(请直接填写答案);
的式子表示出来,从小到大依次是__________、___________、_______________(请直接填写答案);
(2)用(1)中方式被框住的4个数之和可能等于2019吗?如果可能,请求出![]() 的值;如果不可能,请说明理由.
的值;如果不可能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com