
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)判断ABC的形状,并说明理由;
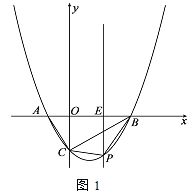
(2)如图1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交x轴于点E.当PBC面积的最大值时,点F为线段BC一点(不与点、重合),连接EF,动点G从点E出发,沿线段EF以每秒1个单位的速度运动到点F,再沿FC以每秒![]() 个单位的速度运动到点C后停止,当点F的坐标是多少时,点G在整个运动过程中用时最少?
个单位的速度运动到点C后停止,当点F的坐标是多少时,点G在整个运动过程中用时最少?
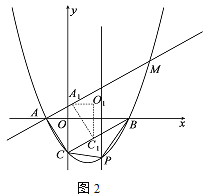
(3)如图2,将ACO沿射线CB方向以每秒![]() 个单位的速度平移,记平移后的ACO为A1C1O1,连接A A1,直线A A1交抛物线与点M,设平移的时间为t秒,当A MC1为等腰三角形时,求t的值.
个单位的速度平移,记平移后的ACO为A1C1O1,连接A A1,直线A A1交抛物线与点M,设平移的时间为t秒,当A MC1为等腰三角形时,求t的值.
【答案】(1)△ABC为直角三角形,理由见解析;(2)![]() ;(3)当△AMC1为等腰三角形时,则t的值t=
;(3)当△AMC1为等腰三角形时,则t的值t=![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】(1)结论:△ABC是直角三角形.在Rt△AOC中,由tan∠ACO=![]() ,推出∠ACO=30°,在Rt△OBC中,由tan∠BCO=
,推出∠ACO=30°,在Rt△OBC中,由tan∠BCO=![]() ,推出∠BCO=60°,可得∠ACB=∠ACO+∠BCO=90°;
,推出∠BCO=60°,可得∠ACB=∠ACO+∠BCO=90°;
(2)设P(m,![]() m2-
m2-![]() m-
m-![]() ),作射线CN,使得∠BCN=60°,作FH⊥CN于H,FG⊥AE于G,则FH=CFcos30°=
),作射线CN,使得∠BCN=60°,作FH⊥CN于H,FG⊥AE于G,则FH=CFcos30°=![]() CF,首先求出点P坐标,动点G的运动时间=
CF,首先求出点P坐标,动点G的运动时间=![]() CF=EF+FH,根据垂线段最短可知,当EH⊥CN时,动点G的运动时间最小,由此即可解决问题;
CF=EF+FH,根据垂线段最短可知,当EH⊥CN时,动点G的运动时间最小,由此即可解决问题;
(3)求出直线AM的解析式,利用方程组求出点M坐标,由题意C′(t,![]() t-
t-![]() ),分三种情形讨论,想办法列出方程即可解决问题;
),分三种情形讨论,想办法列出方程即可解决问题;
(1)结论:△ABC是直角三角形.
理由:如图1中,连接AC.
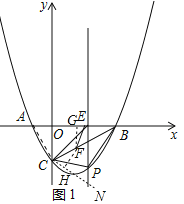
∵抛物线y=![]() x2-
x2-![]() x-
x-![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,
∴A(-1,0),B(3,0),C(0,-![]() ),
),
在Rt△AOC中,∵tan∠ACO=![]() ,
,
∴∠ACO=30°,
在Rt△OBC中,∵tan∠BCO=![]() ,
,
∴∠BCO=60°,
∴∠ACB=∠ACO+∠BCO=90°,
∴△ABC是直角三角形.
(2)设P(m,![]() m2-
m2-![]() m-
m-![]() ),作射线CN,使得∠BCN=60°,作FH⊥CN于H,FG⊥AE于G,则FH=CFcos30°=
),作射线CN,使得∠BCN=60°,作FH⊥CN于H,FG⊥AE于G,则FH=CFcos30°=![]() CF.
CF.
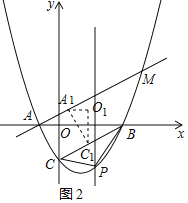
则S△PBC=S△POC+S△POB-S△BOC
=![]() ×
×![]() ×m+
×m+![]() ×3×(-
×3×(-![]() m2+
m2+![]() m+
m+![]() )-
)-![]() ×
×![]() ×3
×3
=-![]() (m-
(m-![]() )2+
)2+ ![]() ,
,
∵-![]() <0,
<0,
∴m=![]() 时,△PBC的面积最大,此时P(
时,△PBC的面积最大,此时P(![]() ,-
,-![]() ),
),
∵动点G的运动时间=![]() CF=EF+FH,
CF=EF+FH,
根据垂线段最短可知,当EH⊥CN时,动点G的运动时间最小,
∵∠EFB=∠EBF=30°,
∴EF=EB=![]() ,
,
在Rt△EFG中,FG=EFcos30°=![]() ,EG=
,EG=![]() ,OG=
,OG=![]() ,
,
∴此时F的坐标为(![]() ,-
,-![]() ).
).
(3)由题意直线BC的解析式为y=![]() x-
x-![]() ,直线AC的解析式为y=
,直线AC的解析式为y=![]() x+
x+![]() ,
,
由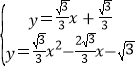 ,
,
解得![]() ,或
,或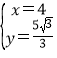
∴M(4,![]() ),
),
∵C1(t,![]() t-
t-![]() ),
),
∴AM2=52+(![]() )2,C1A2=(t+1)2+(
)2,C1A2=(t+1)2+(![]() t-
t-![]() )2,MC1=(4-t)2+(
)2,MC1=(4-t)2+(![]() -
-![]() t+
t+![]() )2,
)2,
①当AM=MC1时,52+(![]() )2=(4-t)2+(
)2=(4-t)2+(![]() -
-![]() t+
t+![]() )2,解得t=5+
)2,解得t=5+![]() 或5-
或5-![]() ,
,
②当C1A=C1M时,(t+1)2+(![]() t-
t-![]() )2=(4-t)2+(
)2=(4-t)2+(![]() -
-![]() t+
t+![]() )2,解得t=
)2,解得t=![]()
③当C1A=AM时,52+(![]() )2=(t+1)2+(
)2=(t+1)2+(![]() t-
t-![]() )2,解得t=
)2,解得t=![]() s或-
s或-![]() (舍弃),
(舍弃),
综上所述,满足条件的t的值为(5+![]() )s或(5-
)s或(5-![]() )s或
)s或![]() s或
s或![]() s.
s.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】根据阅读材料,回答问题.
材料:如图所示,有公共端点(O)的两条射线组成的图形叫做角(![]() ).如果一条射线(
).如果一条射线(![]() )把一个角(
)把一个角(![]() )分成两个相等的角(
)分成两个相等的角(![]() 和
和![]() ),这条射线(
),这条射线(![]() )叫做这个角的平分线.这时,
)叫做这个角的平分线.这时,![]() (或
(或![]() ).
).
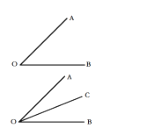
问题:平面内一定点A在直线![]() 的上方,点O为直线
的上方,点O为直线![]() 上一动点,作射线
上一动点,作射线![]() ,
,![]() ,
,![]() ,当点O在直线
,当点O在直线![]() 上运动时,始终保持
上运动时,始终保持![]() ,
,![]() ,将射线
,将射线![]() 绕点O顺时针旋转60°得到射线
绕点O顺时针旋转60°得到射线![]() .
.
(1)如图1,当点O运动到使点A在射线![]() 的左侧时,若
的左侧时,若![]() 平分
平分![]() ,求
,求![]() 的度数;
的度数;
(2)当点O运动到使点A在射线![]() 的左侧,
的左侧,![]() 时,求
时,求![]() 的值;
的值;
(3)当点O运动到某一时刻时,![]() ,直接写出此时
,直接写出此时![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有射线![]() 和点
和点![]() ,
,![]() ,请用尺规按下列要求作图:
,请用尺规按下列要求作图:
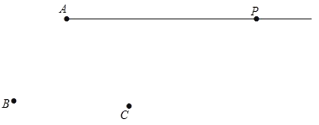
(1)连接![]() ,并在射线
,并在射线![]() 上截取
上截取![]() ;
;
(2)连接![]() 、
、![]() ,并延长
,并延长![]() 到
到![]() ,使
,使![]()
(3)在(2)的基础上,取![]() 中点
中点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
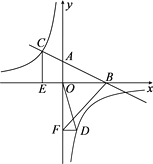
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,![]() ,OB=2,OE=1.
,OB=2,OE=1.
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果SBAF=4SDFO,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
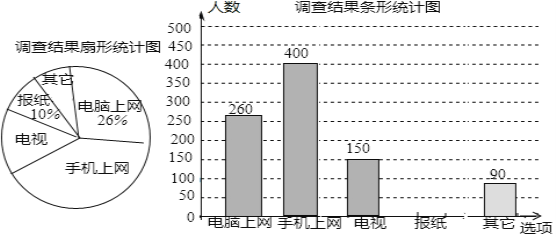
根据以上信息解答下列问题.
(1)这次抽样调查的样本容量是__________.
(2)通过“电视”了解新闻的人数占被调查人数的百分比为______;扇形统计图中,“手机上网”所对应的圆心角的度数是_________.
(3)请补全条形统计图;
(4)若该市约有950万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生开展课外社会实践活动,现有甲、乙两种大客车可租,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,甲种客车每辆载客量45人,乙种客车每辆载客量30人,共有师生330人,求最节省的租车费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
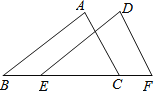
【题目】如图,点B,E,C,F在同一条直线上,AB=DE,∠B=∠DEF.要使△ABC≌△DEF,则需要再添加的一个条件是_______.(写出一个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“水是生命之源”,某市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
月用水量(吨) | 单价(元/吨) |
不超过25吨 | 1.4 |
超过25吨的部分 | 2.1 |
另:每吨用水加收0.95元的城市污水处理费 | |
(1)如果1月份小明家用水量为18吨,那么小明家1月份应该缴纳水费 元;
(2)小明家2月份共缴纳水费104.5元,那么小明家2月份用水多少吨?
(3)小明家的水表3月份出了故障,只有80%的用水量记入水表中,这样小明家在3月份只缴纳了56.4元水费,问小明家3月份实际应该缴纳水费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com