
【题目】如图,直线![]() 相交于点
相交于点![]() ,
,![]() .
.
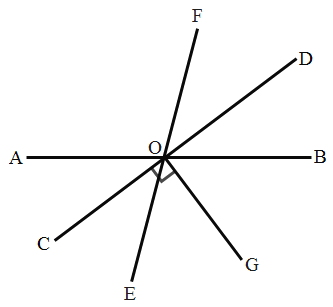
(1)已知![]() ,求
,求![]() 的度数;
的度数;
(2)如果![]() 是
是![]() 的平分线,那么
的平分线,那么![]() 是
是![]() 的平分线吗?说明理由.
的平分线吗?说明理由.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了迎接第二届“环泉州湾国际自行车赛”的到来,泉州台商投资区需要制作宣传单.有两个印刷厂前来联系制作业务,甲厂的优惠条件是:按每份定价1.5元的八折收费,另收900元制版费;乙厂的优惠条件是:每份定价1.5元的价格不变,而制版费900元则六折优惠.且甲乙两厂都规定:一次印刷数量至少是500份.
(1)若印刷数量为![]() 份(
份(![]() ,且
,且![]() 是整数),请你分别写出两个印刷厂收费的代数式;
是整数),请你分别写出两个印刷厂收费的代数式;
(2)如果比赛宣传单需要印刷1100份,应选择哪个厂家?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比、转化等数学思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
已知![]() .
.
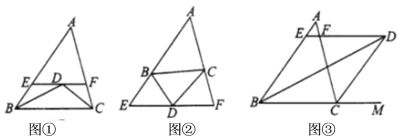
(1)观察发现
如图①,若点![]() 是
是![]() 和
和![]() 的角平分线的交点,过点
的角平分线的交点,过点![]() 作
作![]() 分别交
分别交![]() 、
、![]() 于、
于、![]() ,
,![]() 填空:
填空: ![]() 与
与![]() 、
、![]() 的数量关系是________________________________________.
的数量关系是________________________________________.
(2)猜想论证
如图②,若![]() 点是外角
点是外角![]() 和
和![]() 的角平分线的交点,其他条件不变,填:
的角平分线的交点,其他条件不变,填: ![]() 与
与![]() 、
、![]() 的数量关系是_____________________________________.
的数量关系是_____________________________________.
(3)类比探究
如图③,若点![]() 是
是![]() 和外角
和外角![]() 的角平分线的交点.其他条件不变,则(1)中的关系成立吗?若成立,请加以证明;若不成立,请写出关系式,再证明.
的角平分线的交点.其他条件不变,则(1)中的关系成立吗?若成立,请加以证明;若不成立,请写出关系式,再证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)判断ABC的形状,并说明理由;
(2)如图1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交x轴于点E.当PBC面积的最大值时,点F为线段BC一点(不与点、重合),连接EF,动点G从点E出发,沿线段EF以每秒1个单位的速度运动到点F,再沿FC以每秒![]() 个单位的速度运动到点C后停止,当点F的坐标是多少时,点G在整个运动过程中用时最少?
个单位的速度运动到点C后停止,当点F的坐标是多少时,点G在整个运动过程中用时最少?
(3)如图2,将ACO沿射线CB方向以每秒![]() 个单位的速度平移,记平移后的ACO为A1C1O1,连接A A1,直线A A1交抛物线与点M,设平移的时间为t秒,当A MC1为等腰三角形时,求t的值.
个单位的速度平移,记平移后的ACO为A1C1O1,连接A A1,直线A A1交抛物线与点M,设平移的时间为t秒,当A MC1为等腰三角形时,求t的值.
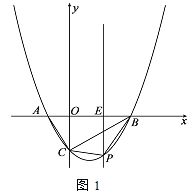
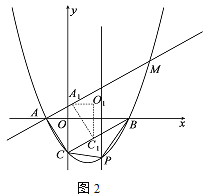
查看答案和解析>>
科目:初中数学 来源: 题型:
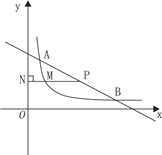
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于A,B两点,A点的横坐标为2.
交于A,B两点,A点的横坐标为2.
(1)求点B的坐标;
(2)P为线段AB上一点(不包括端点),P点的纵坐标为a,作PN⊥y轴,垂足为N,交双曲线于点M,求![]() 的最大值;
的最大值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:用若干个边长为1的小等边三角形拼成![]() 层的大等边三角形,共需要多少个小等边三角形?共有线段多少条?
层的大等边三角形,共需要多少个小等边三角形?共有线段多少条?
图①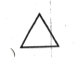 图②
图② 图③
图③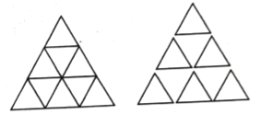
问题探究:
如图①,是一个边长为1的等边三角形,现在用若干个这样的等边三角形再拼成更大的等边三角形.
(1)用图①拼成两层的大等边三角形,如图②,从上往下,第一层有1个,第二层有2个,共用了![]() 个图①的等边三角形,则有长度为1的线段
个图①的等边三角形,则有长度为1的线段![]() 条;还有边长为2的等边三角形1个,则有长度为2的线段
条;还有边长为2的等边三角形1个,则有长度为2的线段![]() 条;所以,共有线段
条;所以,共有线段![]() 条.
条.
(2)用图①拼成三层的大等边三角形,如图③,从上往下,第一层有1个,第二层有2个,第三层有3个,共用了![]() 个图①的等边三角形,则有长度为1的线段
个图①的等边三角形,则有长度为1的线段![]() 条;还有边长为2的等边三角形
条;还有边长为2的等边三角形![]() 个,则有长度为2的线段
个,则有长度为2的线段![]() 条;还有边长为3的等边三角形1个,则有长度为3的线段
条;还有边长为3的等边三角形1个,则有长度为3的线段![]() 条;所以,共有线段
条;所以,共有线段![]() 条.……
条.……
问题解决:
(3)用图①拼成四层的大等边三角形,共需要多少个图①三角形?共有线段多少条?请在方框中画出一个示意图,并写出探究过程;
(4)用图①拼成20层的大等边三角形,共用了 个图①三角形,共有线段 条;
(5)用图①拼成![]() 层的大等边三角形,共用了 个图①三角形,共有线段 条,其中边长为2的等边三角形共有 个.
层的大等边三角形,共用了 个图①三角形,共有线段 条,其中边长为2的等边三角形共有 个.
(6)拓展提升:如果用边长为3的小等边三角形拼成边长为30的大等边三角形,共需要 个小等边三角形,共有线段 条.
查看答案和解析>>
科目:初中数学 来源: 题型:
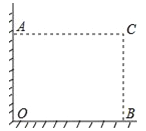
【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com