
【题目】类比、转化等数学思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
已知![]() .
.
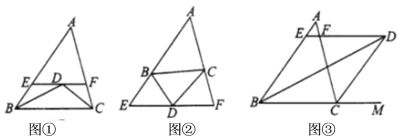
(1)观察发现
如图①,若点![]() 是
是![]() 和
和![]() 的角平分线的交点,过点
的角平分线的交点,过点![]() 作
作![]() 分别交
分别交![]() 、
、![]() 于、
于、![]() ,
,![]() 填空:
填空: ![]() 与
与![]() 、
、![]() 的数量关系是________________________________________.
的数量关系是________________________________________.
(2)猜想论证
如图②,若![]() 点是外角
点是外角![]() 和
和![]() 的角平分线的交点,其他条件不变,填:
的角平分线的交点,其他条件不变,填: ![]() 与
与![]() 、
、![]() 的数量关系是_____________________________________.
的数量关系是_____________________________________.
(3)类比探究
如图③,若点![]() 是
是![]() 和外角
和外角![]() 的角平分线的交点.其他条件不变,则(1)中的关系成立吗?若成立,请加以证明;若不成立,请写出关系式,再证明.
的角平分线的交点.其他条件不变,则(1)中的关系成立吗?若成立,请加以证明;若不成立,请写出关系式,再证明.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)不成立,
;(3)不成立, ![]() ,证明详见解析.
,证明详见解析.
【解析】
(1)根据平行线的性质与角平分线的定义得出∠EDB=∠EBD,∠FCD=∠FDC,从而得出EF与BE、CF的数量关系;
(2)根据平行线的性质与角平分线的定义得出∠EDB=∠EBD,∠FCD=∠FDC,从而得出EF与BE、CF的数量关系;
(3)根据平行线的性质与角平分线的定义得出EF与BE、CF的数量关系.
(1)EF=BE+CF.
∵点D是∠ABC和∠ACB的角平分线的交点,
∴∠EBD=∠DBC,∠FCD=∠DCB.
∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB.
∴∠EDB=∠EBD,∠FCD=∠FDC.
∴EB=ED,DF=CF.
∴EF=BE+CF.
故本题答案为:EF=BE+CF.
(2)EF=BE+CF.
∵D点是外角∠CBE和∠BCF的角平分线的交点,
∴∠EBD=∠DBC,∠FCD=∠DCB.
∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCB.
∴∠EDB=∠EBD,∠FCD=∠FDC.
∴EB=ED,DF=CF.
∴EF=BE+CF.
故本题答案为:EF=BE+CF.
(3)不成立;EF=BECF,证明详见解析.
∵点D是∠ABC和外角∠ACM的角平分线的交点,
∴∠EBD=∠DBC,∠ACD=∠DCM.
∵EF∥BC,
∴∠EDB=∠DBC,∠FDC=∠DCM.
∴∠EBD=∠EDB,∠FDC=∠FCD.
∴BE=ED,FD=FC.
∵EF=EDFD,
∴EF=BECF.


科目:初中数学 来源: 题型:
【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的有( )
①用两颗钉子就可以把木条固定在墙上
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上。
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.
阅读材料:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知:![]() ,求代数式
,求代数式![]() 的值.
的值.
解:因为![]() ,所以
,所以![]() ,
,
即![]() ,即
,即![]() ,
,
所以 .
.
根据材料回答问题(直接写出答案):
(1)已知![]() ,则
,则![]() _______.
_______.
(2)解分式方程组 ,解得,方程组的解为_______.
,解得,方程组的解为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有射线![]() 和点
和点![]() ,
,![]() ,请用尺规按下列要求作图:
,请用尺规按下列要求作图:
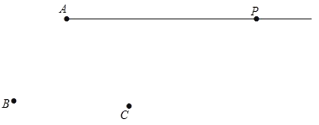
(1)连接![]() ,并在射线
,并在射线![]() 上截取
上截取![]() ;
;
(2)连接![]() 、
、![]() ,并延长
,并延长![]() 到
到![]() ,使
,使![]()
(3)在(2)的基础上,取![]() 中点
中点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,中途与乙相遇后休息了一会儿,然后以原来的速度继续行驶直到A地.设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示,则乙车到达A地时甲车距B地的路程为___________ 千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,![]() ,OB=2,OE=1.
,OB=2,OE=1.
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果SBAF=4SDFO,求点D的坐标.
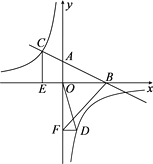
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上一点,且AD∥OC
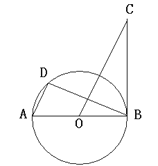
(1)求证:△ADB∽△OBC;
(2)若AB=2,BC=![]() ,求AD的长(结果保留根号).
,求AD的长(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com