
【题目】在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.
阅读材料:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知:![]() ,求代数式
,求代数式![]() 的值.
的值.
解:因为![]() ,所以
,所以![]() ,
,
即![]() ,即
,即![]() ,
,
所以 .
.
根据材料回答问题(直接写出答案):
(1)已知![]() ,则
,则![]() _______.
_______.
(2)解分式方程组 ,解得,方程组的解为_______.
,解得,方程组的解为_______.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线![]() 相交于A,B两点,A点坐标为(-3,2),B点坐标为(n,-3).
相交于A,B两点,A点坐标为(-3,2),B点坐标为(n,-3).
(1)求一次函数和反比例函数表达式;
(2)如果点P是x轴上一点,且△ABP的面积是5,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接第二届“环泉州湾国际自行车赛”的到来,泉州台商投资区需要制作宣传单.有两个印刷厂前来联系制作业务,甲厂的优惠条件是:按每份定价1.5元的八折收费,另收900元制版费;乙厂的优惠条件是:每份定价1.5元的价格不变,而制版费900元则六折优惠.且甲乙两厂都规定:一次印刷数量至少是500份.
(1)若印刷数量为![]() 份(
份(![]() ,且
,且![]() 是整数),请你分别写出两个印刷厂收费的代数式;
是整数),请你分别写出两个印刷厂收费的代数式;
(2)如果比赛宣传单需要印刷1100份,应选择哪个厂家?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣2,1),B(1,4),若反比例函数y=![]() 与线段AB有公共点时,k的取值范围是( )
与线段AB有公共点时,k的取值范围是( )
A. ﹣![]() ≤k<0或0<k≤4 B. k≤﹣2或k≥4
≤k<0或0<k≤4 B. k≤﹣2或k≥4
C. ﹣2≤k<0或k≥4 D. ﹣2≤k<0或0<k≤4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下数表是由从1开始的连续自然数组成,观察规律并完成各题的填空.
(1)表中第6行的最后一个数是_____,第n行的最后一个数是_____;
(2)若用(a,b)表示一个数在数表中的位置,如9的位置是(4,3),则2018所在的位置是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
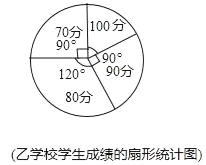
【题目】在“学科能力”展示活动中,某县教育局决定在甲、乙两校举行“学科能力”比赛活动,规定甲、乙两学校选派相同人数的选手参加,比赛结束后,发现参赛选手的成绩是70分、80分、90分、l00分这四种成绩中的一种,已知甲、乙两校的选手获得100分的人数相等.现根据甲、乙两校选手的成绩,绘制成两幅不完整统计图如下:
(1)请补全条形统计图;
(2)比赛结束后,教育局决定对甲、乙两校获得100分的选手进行集中培训,培训后,从中随机选取两位选手参加市里的决赛,请用列表法或画树状图的方法,求所选两位选手来自同一学校的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比、转化等数学思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
已知![]() .
.
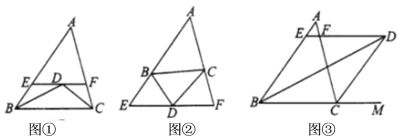
(1)观察发现
如图①,若点![]() 是
是![]() 和
和![]() 的角平分线的交点,过点
的角平分线的交点,过点![]() 作
作![]() 分别交
分别交![]() 、
、![]() 于、
于、![]() ,
,![]() 填空:
填空: ![]() 与
与![]() 、
、![]() 的数量关系是________________________________________.
的数量关系是________________________________________.
(2)猜想论证
如图②,若![]() 点是外角
点是外角![]() 和
和![]() 的角平分线的交点,其他条件不变,填:
的角平分线的交点,其他条件不变,填: ![]() 与
与![]() 、
、![]() 的数量关系是_____________________________________.
的数量关系是_____________________________________.
(3)类比探究
如图③,若点![]() 是
是![]() 和外角
和外角![]() 的角平分线的交点.其他条件不变,则(1)中的关系成立吗?若成立,请加以证明;若不成立,请写出关系式,再证明.
的角平分线的交点.其他条件不变,则(1)中的关系成立吗?若成立,请加以证明;若不成立,请写出关系式,再证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:用若干个边长为1的小等边三角形拼成![]() 层的大等边三角形,共需要多少个小等边三角形?共有线段多少条?
层的大等边三角形,共需要多少个小等边三角形?共有线段多少条?
图①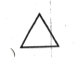 图②
图② 图③
图③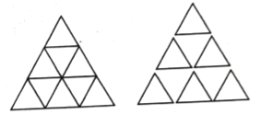
问题探究:
如图①,是一个边长为1的等边三角形,现在用若干个这样的等边三角形再拼成更大的等边三角形.
(1)用图①拼成两层的大等边三角形,如图②,从上往下,第一层有1个,第二层有2个,共用了![]() 个图①的等边三角形,则有长度为1的线段
个图①的等边三角形,则有长度为1的线段![]() 条;还有边长为2的等边三角形1个,则有长度为2的线段
条;还有边长为2的等边三角形1个,则有长度为2的线段![]() 条;所以,共有线段
条;所以,共有线段![]() 条.
条.
(2)用图①拼成三层的大等边三角形,如图③,从上往下,第一层有1个,第二层有2个,第三层有3个,共用了![]() 个图①的等边三角形,则有长度为1的线段
个图①的等边三角形,则有长度为1的线段![]() 条;还有边长为2的等边三角形
条;还有边长为2的等边三角形![]() 个,则有长度为2的线段
个,则有长度为2的线段![]() 条;还有边长为3的等边三角形1个,则有长度为3的线段
条;还有边长为3的等边三角形1个,则有长度为3的线段![]() 条;所以,共有线段
条;所以,共有线段![]() 条.……
条.……
问题解决:
(3)用图①拼成四层的大等边三角形,共需要多少个图①三角形?共有线段多少条?请在方框中画出一个示意图,并写出探究过程;
(4)用图①拼成20层的大等边三角形,共用了 个图①三角形,共有线段 条;
(5)用图①拼成![]() 层的大等边三角形,共用了 个图①三角形,共有线段 条,其中边长为2的等边三角形共有 个.
层的大等边三角形,共用了 个图①三角形,共有线段 条,其中边长为2的等边三角形共有 个.
(6)拓展提升:如果用边长为3的小等边三角形拼成边长为30的大等边三角形,共需要 个小等边三角形,共有线段 条.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com