
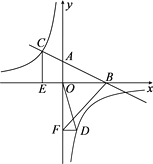
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,![]() ,OB=2,OE=1.
,OB=2,OE=1.
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果SBAF=4SDFO,求点D的坐标.
【答案】(l) y=![]() ;(2) D(
;(2) D(![]() ,-2).
,-2).
【解析】(1)由边的关系可得出BE=6,通过解直角三角形可得出CE=3,结合函数图象即可得出点C的坐标,再根据点C的坐标利用反比例函数图象上点的坐标特征,即可求出反比例函数系数m,由此即可得出结论;
(2)由点D在反比例函数在第四象限的图象上,设出点D的坐标为(n,-![]() )(n>0).通过解直角三角形求出线段OA的长度,再利用三角形的面积公式利用含n的代数式表示出S△BAF,根据点D在反比例函数图形上利用反比例函数系数k的几何意义即可得出S△DFO的值,结合题意给出的两三角形的面积间的关系即可得出关于n的分式方程,解方程,即可得出n值,从而得出点D的坐标.
)(n>0).通过解直角三角形求出线段OA的长度,再利用三角形的面积公式利用含n的代数式表示出S△BAF,根据点D在反比例函数图形上利用反比例函数系数k的几何意义即可得出S△DFO的值,结合题意给出的两三角形的面积间的关系即可得出关于n的分式方程,解方程,即可得出n值,从而得出点D的坐标.
(1)∵OB=2,OE=1,
∴BE=OB+OE=3.
∵CE⊥x轴,
∴∠CEB=90°.
在Rt△BEC中,∠CEB=90°,BE=3,sin∠ABO=![]() ,
,
∴tan∠ABO=![]() ,
,
∴CE=BEtan∠ABO=3×![]() =
=![]() ,
,
结合函数图象可知点C的坐标为(-1,![]() ).
).
∵点C在反比例函数y=![]() 的图象上,
的图象上,
∴k=-1×![]() =-
=-![]() ,
,
∴反比例函数的解析式为y=-![]() .
.
(2)∵点D在反比例函数y=-![]() 第四象限的图象上,
第四象限的图象上,
∴设点D的坐标为(n,-![]() )(n>0).
)(n>0).
在Rt△AOB中,∠AOB=90°,OB=4,tan∠ABO=![]() ,
,
∴OA=OBtan∠ABO=2×![]() =1.
=1.
∵S△BAF=![]() AFOB=
AFOB=![]() (OA+OF)OB=
(OA+OF)OB=![]() (1+
(1+![]() )×2=1+
)×2=1+![]() .
.
∵点D在反比例函数y=-![]() 第四象限的图象上,
第四象限的图象上,
∴S△DFO=![]() ×|-
×|-![]() |=
|=![]() .
.
∵S△BAF=4S△DFO,
∴1+![]() =4×
=4×![]() ,
,
解得:n=![]() ,
,
经验证,n=![]() 是分式方程的解,
是分式方程的解,
∴点D的坐标为(![]() ,-2).
,-2).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
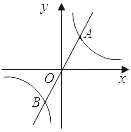
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() 交于A、B两点,且点A的横坐标为
交于A、B两点,且点A的横坐标为![]() .
.
(1)求k的值;
(2)若双曲线y=![]() 上点C的纵坐标为3,求△AOC的面积;
上点C的纵坐标为3,求△AOC的面积;
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=![]() 上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下数表是由从1开始的连续自然数组成,观察规律并完成各题的填空.
(1)表中第6行的最后一个数是_____,第n行的最后一个数是_____;
(2)若用(a,b)表示一个数在数表中的位置,如9的位置是(4,3),则2018所在的位置是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比、转化等数学思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
已知![]() .
.
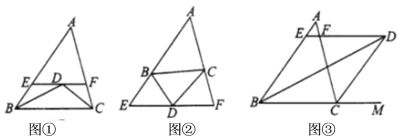
(1)观察发现
如图①,若点![]() 是
是![]() 和
和![]() 的角平分线的交点,过点
的角平分线的交点,过点![]() 作
作![]() 分别交
分别交![]() 、
、![]() 于、
于、![]() ,
,![]() 填空:
填空: ![]() 与
与![]() 、
、![]() 的数量关系是________________________________________.
的数量关系是________________________________________.
(2)猜想论证
如图②,若![]() 点是外角
点是外角![]() 和
和![]() 的角平分线的交点,其他条件不变,填:
的角平分线的交点,其他条件不变,填: ![]() 与
与![]() 、
、![]() 的数量关系是_____________________________________.
的数量关系是_____________________________________.
(3)类比探究
如图③,若点![]() 是
是![]() 和外角
和外角![]() 的角平分线的交点.其他条件不变,则(1)中的关系成立吗?若成立,请加以证明;若不成立,请写出关系式,再证明.
的角平分线的交点.其他条件不变,则(1)中的关系成立吗?若成立,请加以证明;若不成立,请写出关系式,再证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
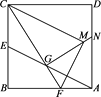
【题目】在正方形ABCD中,AB=![]() ,E是边BC的中点,F是AB上一点,线段AE、CF交于点G,且CE=EG,将ABF沿CF翻折,使得点B落在点M,连接GM并延长交AD于点N,则AGN的面积为_________________.
,E是边BC的中点,F是AB上一点,线段AE、CF交于点G,且CE=EG,将ABF沿CF翻折,使得点B落在点M,连接GM并延长交AD于点N,则AGN的面积为_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
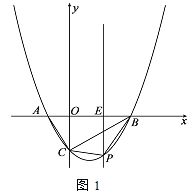
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)判断ABC的形状,并说明理由;
(2)如图1,点P为直线BC下方的二次函数图象上的一个动点(点P与B、C不重合),过点P作y轴的平行线交x轴于点E.当PBC面积的最大值时,点F为线段BC一点(不与点、重合),连接EF,动点G从点E出发,沿线段EF以每秒1个单位的速度运动到点F,再沿FC以每秒![]() 个单位的速度运动到点C后停止,当点F的坐标是多少时,点G在整个运动过程中用时最少?
个单位的速度运动到点C后停止,当点F的坐标是多少时,点G在整个运动过程中用时最少?
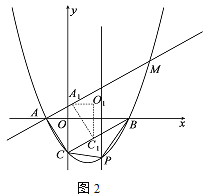
(3)如图2,将ACO沿射线CB方向以每秒![]() 个单位的速度平移,记平移后的ACO为A1C1O1,连接A A1,直线A A1交抛物线与点M,设平移的时间为t秒,当A MC1为等腰三角形时,求t的值.
个单位的速度平移,记平移后的ACO为A1C1O1,连接A A1,直线A A1交抛物线与点M,设平移的时间为t秒,当A MC1为等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
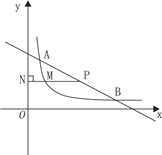
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于A,B两点,A点的横坐标为2.
交于A,B两点,A点的横坐标为2.
(1)求点B的坐标;
(2)P为线段AB上一点(不包括端点),P点的纵坐标为a,作PN⊥y轴,垂足为N,交双曲线于点M,求![]() 的最大值;
的最大值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点
上的一个动点![]() ,点
,点![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.

(1)若点![]() 恰好是
恰好是![]() 的中点,则
的中点,则![]() _______
_______![]() ;若
;若![]() ,则
,则![]() _________
_________![]() ;
;
(2)随着点![]() 位置的改版,
位置的改版,![]() 的长是否会改变?如果改变,请说明原因;如果不变,请求出的长;
的长是否会改变?如果改变,请说明原因;如果不变,请求出的长;
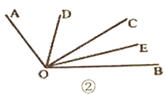
(3)知识迁移:如图②,已知![]() ,过角的内部任意一点
,过角的内部任意一点![]() 画射线
画射线![]() ,若
,若![]() 分别平分
分别平分![]() 和
和![]() ,试说明
,试说明![]() 的度数与射线
的度数与射线![]() 的位置无关.
的位置无关.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com