
【题目】如图,已知![]() ,
, ![]() ,且
,且![]() ,
,![]() 满足
满足![]() ,
,![]() 为第一象限内一点,连接
为第一象限内一点,连接![]() ,连接
,连接![]() 交
交![]() 轴于
轴于![]() 点,且
点,且![]() .
.
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
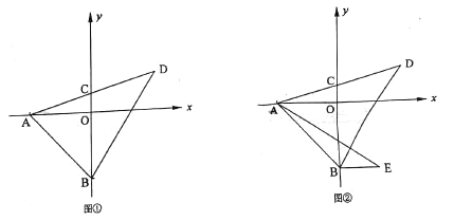
(2)如图①,若![]() 的面积为20,求
的面积为20,求![]() 点的坐标;
点的坐标;
(3)如图②,在第四象限内过点![]() 作
作![]() 轴,且
轴,且![]() ,连接
,连接![]() .求证:
.求证:![]() , 且
, 且![]() .
.
【答案】(1)点A坐标为(-4,0),点B的坐标为(0,-4);(2)点D的坐标为(4,2);(3)见解析
【解析】
(1)根据平方和绝对值的非负性即可得出结论;
(2)过点D作DE⊥y轴,利用AAS证出△DEC≌△AOC,从而得出DE=AO=4,S△DEC=S△AOC,然后根据已知面积即可求出OE的长,从而求出结论;
(3)利用SAS证出△ABE≌BFD,从而得出![]() ,∠EAB=∠DBF,然后根据三角形外角的性质和等量代换即可得出结论.
,∠EAB=∠DBF,然后根据三角形外角的性质和等量代换即可得出结论.
解:(1)∵![]() ,
,![]()
∴![]()
解得:a=b=-4
∴点A坐标为(-4,0),点B的坐标为(0,-4)
(2)过点D作DE⊥y轴于E
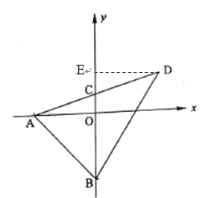
∴∠DEC=∠AOC=90°
在△DEC和△AOC中
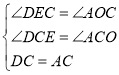
∴△DEC≌△AOC
∴DE=AO=4,S△DEC=S△AOC
∵![]() 的面积为20
的面积为20
∴S△AOB+S△AOC+S△DCB=20
∴S△AOB+S△DEC+S△DCB=20
∴S△AOB+S△DEB=20
∴![]() OA·OB+
OA·OB+![]() BE·DE=20
BE·DE=20
∴![]() ×4×4+
×4×4+![]() BE×4=20
BE×4=20
解得:BE=6
∴OE=BE-OB=2
∴点D的坐标为(4,2)
(3)过点D作DF⊥x轴于F,连接BF,设BD与AE交于点G
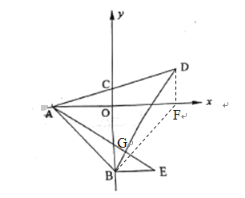
∴DF∥OC
∵AC=CD
∴AO=OF
∴OB垂直平分AF,DF=2OC
∴AB=BF
∴∠BAF=∠BFA
∵OA=OB,∠AOB=90°
∴∠BAF=∠OBA=45°
∴△ABF为等腰直角三角形,∠ABF=90°
∴∠ABE=135°,∠BFD=135°
∴∠ABE=∠BFD
∵![]()
∴BE=DF
在△ABE和△BFD中
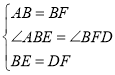
∴△ABE≌BFD
∴![]() ,∠EAB=∠DBF
,∠EAB=∠DBF
∴∠BGE=∠EAB+∠GBA=∠DBF+∠GBA=∠ABF=90°
∴![]()


科目:初中数学 来源: 题型:
【题目】某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1.在温室内,沿前侧内墙保留3m宽的空地,其它三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时,蔬菜种植区域的面积是288m2?

查看答案和解析>>
科目:初中数学 来源: 题型:
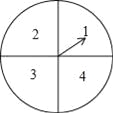
【题目】某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.
(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;
(2)某顾客参加一次抽奖,能获得返还现金的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:![]() 三角形的内心是三角形内切圆的圆心;
三角形的内心是三角形内切圆的圆心;![]() 三角形的外心是三角形三边垂直平分线的交点;
三角形的外心是三角形三边垂直平分线的交点;![]() 平分弦的直径垂直于这条弦;
平分弦的直径垂直于这条弦;![]() 平面上任意三点确定一个圆
平面上任意三点确定一个圆![]() 圆内接四边形的对角互补
圆内接四边形的对角互补![]() 其中,真命题有().
其中,真命题有().
A. 两个 B. 三个 C. 四个 D. 五个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列的网格图中.每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读材料,并完成相应的任务.
阿波罗尼奥斯(约公元前262~190年),古希腊数学家,与欧几里得、阿基米德齐名.他的著作《圆锥曲线论》是古代世界光辉的科学成果,可以说是代表了希腊几何的最高水平.阿波罗尼奧斯定理,是欧氏几何的定理,表述三角形三边和中线的长度关系,即三角形任意两边的平方和等于第三边的一半与该边中线的平方和的2倍.
(1)下面是该结论的部分证明过程,请在框内将其补充完整;
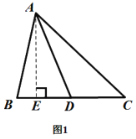
已知:如图1所示,在锐角![]() 中,
中,![]() 为中线..
为中线..
求证:![]()
证明:过点![]() 作
作![]() 于点
于点![]()
![]() 为中线
为中线
![]()
设![]() ,
,![]() ,
,![]()
![]() ,
,![]()
在![]() 中,
中,![]()
在![]() 中,
中,![]() __________
__________
在![]() 中,
中,![]() __________
__________
![]() __________
__________
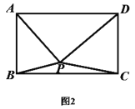
(2)请直接利用阿波罗尼奧斯定理解决下面问题:
如图2,已知点![]() 为矩形
为矩形![]() 内任一点,
内任一点,
求证:![]() (提示:连接
(提示:连接![]() 、
、![]() 交于点
交于点![]() ,连接
,连接![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A、B重合),另一直角边与∠CBM的平分线BF相交于点F.

(1)如图1,当点E在AB边得中点位置时:
①通过测量DE、EF的长度,猜想DE与EF满足的数量关系是 .
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ,请证明你的猜想.
(2)如图2,当点E在AB边上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
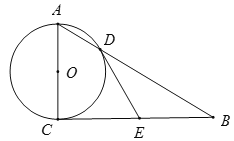
【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系:_________;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC=_______时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com