
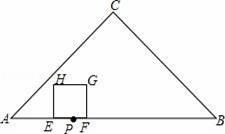
如图,在△ABC中,∠C=90°,AC=BC,AB=20,点P在AB上,AP=6.点E以每秒2个单位长度的速度,从点P出发沿线段PA向点A作匀速运动,点F同时以每秒1个单位长度的速度,从点P出发沿线段PB向点B作匀速运动,点E到达点A后立刻以原速度沿线段AB向点B运动,点F运动到点B时,点E随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分的面积为S.
(1)当t=1时,正方形EFGH的边长是 3 ;当t=4时,正方形EFGH的边长是 8 ;
(2)当0<t≤3时,求S与t的函数关系式.

【考点】相似形综合题;等腰三角形的判定与性质;正方形的性质.
【分析】(1)当t=1时,根据PE=2t,PF=t即可求出EF的值,当t=4时,点E运动到点A后返回,PE=2AP﹣2t,PF=t,由此即可求出EF的值;
(2)当点H在线段AC上时,可求出t=
 ,可分两种情况讨论:当0<t≤
,可分两种情况讨论:当0<t≤
 时,S=S正方形EFGH=EF2,只需用t的代数式表示出EF即可解决问题;当
时,S=S正方形EFGH=EF2,只需用t的代数式表示出EF即可解决问题;当
 <t≤3时,S=S五边形EFGMN=S正方形EFGH﹣S△MHN=EF2﹣
<t≤3时,S=S五边形EFGMN=S正方形EFGH﹣S△MHN=EF2﹣
 HN•HM,只需用t的代数式分别表示出EF、HN、HM即可解决问题.
HN•HM,只需用t的代数式分别表示出EF、HN、HM即可解决问题.
【解答】解:(1)当t=1时,PE=2×1=2,PF=1×1=1,EF=EP+PF=2+1=3.
当t=4时,PE=12﹣2×4=4,PF=1×4=4,EF=EP+PF=4+4=8.
故答案分别为:3、8;
(2)当点H在线段AC上时,
则有AE=HE=EF,即6﹣2t=3t,
解得:t=
 .
.
①当0<t≤
 时,
时,
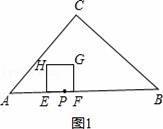

EF=EP+PF=2t+t=3t,
则S=9t2;
②当
 <t≤3时,
<t≤3时,
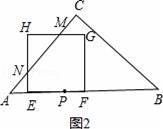

∵∠C=90°,AC=BC,
∴∠A=45°.
∵四边形EFGH是正方形,
∴HE=EF=3t,∠H=∠HEF=90°,
∴∠ANE=90°﹣45°=45°,
∴∠ANE=∠A=45°,
∴NE=AE=AP﹣EP=6﹣2t,
∴HN=HE﹣NE=3t﹣(6﹣2t)=5t﹣6.
∵∠HNM=∠ANE=45°,
∴∠HMN=90°﹣45°=45°,
∴∠HMN=∠HNM=45°,
∴HM=HN=5t﹣6,
∴S=S正方形EFGH﹣S△NHM
=(3t)2﹣
 (5t﹣6)2
(5t﹣6)2
=﹣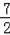
 t2+30t﹣18.
t2+30t﹣18.
综上所述:S与t的函数关系式为
S=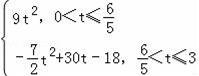
 .
.


科目:初中数学 来源: 题型:
下列从左到右的变形属于因式分解的是()
A.x2+5x-1=x(x+5)-1 B.x2-9=(x+3)(x-3)
C.x2-4+3x=(x+2)(x-2)+3x D.(x+2)(x-2)=x2-4
查看答案和解析>>
科目:初中数学 来源: 题型:
某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
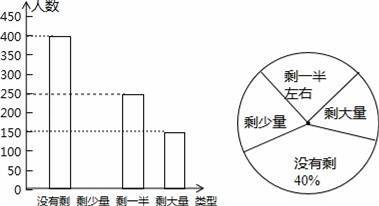

(1)这次被调查的同学共有 名;“剩大量”的扇形圆心角是 .
(2)把条形统计图补充完整;
(3)在被调查的学生中随机抽取一名恰巧是“剩少量”或“剩一半左右”饭的概率多大;
(4)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐.据此估算,该校18 000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(4,0),点C在y的正半轴上,且OB=2OC,在直角坐标平面内确定点D,使得以点D、A、B、C为顶点的四边形是平行四边形,请写出点D的坐标为 .
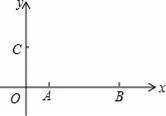

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com